U - критерий Манна-Уитнн

Назначение критерия

Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n1,n2 ≥3 или n1=2, n2≥5. И является более мощным, чем критерий Розенбаума.

Описание критерия

Существует несколько способов использования критерия и несколько вариантов таблиц критических значений, соответствующих этим способам (Гублер Е. В., 1978; Рунион Р., 1982; Захаров В. П.Р 1985; McCall R., 1970; Krauth J., 1988).

Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2-м рядом - тот, где они предположительно ниже.

Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок (Welkowitz J. et al., 1982).

Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше Uэмп,  тем более вероятно, что различия достоверны.

Гипотезы

H0: Уровень признака в группе 2 не ниже уровня признака

в группе 1.

H1: Уровень признака в группе 2 ниже уровня признака

в группе 1.

Графическое представление критерия U

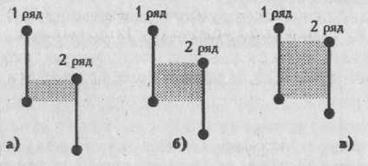
На Рис. 2.5. представлены три из множества возможных вариантов соотношения двух рядов значений.

В варианте (а) второй ряд ниже первого, и ряды почти не перекрещиваются. Область наложения слишком мала, чтобы скрадывать различия между рядами. Есть шанс, что различия между ними достоверны. Точно определить это мы сможем с помощью критерия U.

В варианте (б) второй ряд тоже ниже первого, но и область перекрещивающихся значений у двух рядов достаточно обширна. Она может еще не достигать критической величины, когда различия придется признать несущественными. Но так ли это, можно определить только путем точного подсчета критерия U.

В варианте (в) второй ряд ниже первого, но область наложения настолько обширна, что различия между рядами скрадываются.

Рис. 2.5. Возможные варианты соотношении рядов значений в двух выборках; штриховкой обозначены зоны наложения

Ограничения критерия U

1.  В каждой выборке должно быть не менее 3 наблюдении:

 n1,n2 ≥3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.

2.  В каждой выборке должно быть не более 60 наблюдений; Однако уже при n1,n2 >20 ранжирование становится достаточно трудоемким.

На наш взгляд, в случае, если n1,n2 >20, лучше использовать другой критерий, а именно угловое преобразование Фишера в комбинации с критерием λ, позволяющим выявить критическую точку, в которой накапливаются максимальные различия между двумя сопоставляемыми выборками. Формулировка звучит сложно, но сам метод достаточно прост. Каждому исследователю лучше попробовать разные пути и выбрать тот, который кажется ему более подходящим.

Пример

Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. С помощью критерия Q Розенбаума мы в предыдущем параграфе смогли с высоким уровнем значимости определить, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли этот результат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в Табл. 2.3.

Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?

Таблица 2.3

Индивидуальные значения невербального интеллекта в выборках студентов физического (n1 =14) и психологического (n2=12)  факультетов

Критерий U требует тщательности и внимания. Прежде всего, необходимо помнить правила ранжирования.

Правила ранжирования

1.         Меньшему значению начисляется меньший ранг.

Наименьшему значению начисляется ранг 1.

Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если п=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.

2.         В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:

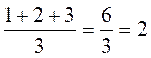
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:

 и т.д.

3.         Общая сумма рангов должка совпадать с расчетной, которая определяется по формуле:

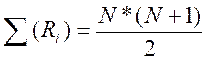
где N – общее количество ранжируемых наблюдений (значений).

Несовпадение реальной и расчётной сумм рангов будет свидетельствовать об ошибке, допущенной  при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить её.

При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.

АЛГОРИТМ 4

Подсчет критерия U Манна-Уитни

1.Перенести все данные испытуемых на индивидуальные карточки.

2.Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 - другим, например, синим.

3.Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.

4.Проранжировать значения на карточках, приписывая меньшему значению меньший ранг. Всего рангов получится столько, сколько у нас (n1 +n2).

5.Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой.

6.Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.

7.Определить большую из двух ранговых сумм.

8.Определить значение U по формуле:

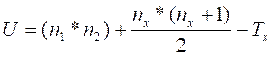
где n1 - количество испытуемых в выборке 1;

n2 - количество испытуемых в выборке 2;

Тх - большая из двух ранговых сумм;

nx - количество испытуемых в группе с большей суммой рангов. 9. Определить критические значения U по Табл. II Приложения

Если Uэмп >UKp 0,05, Н0 принимается.

Если Uэмп ≤UKp 0,05, Но отвергается. Чем меньше значения U, тем

достоверность различий выше.

Теперь проделаем всю эту работу на материале данного примера. В результате работы по 1-6 шагам алгоритма построим таблицу.

Таблица 2.4

Подсчет ранговых сумм по выборкам студентов физического и психологического факультетов

Общая сумма рангов: 165+186=351.

Расчетная сумма:

Равенство реальной и расчетной сумм соблюдено.

Мы видим, что по уровню невербального интеллекта более "высоким" рядом оказывается выборка студентов-психологов.

Именно на эту выборку приходится большая ранговая сумма: 186.

Теперь мы готовы сформулировать гипотезы:

H0: Группа студентов-психологов не превосходит группу студентов-физиков по уровню невербального интеллекта.

H1:   Группа   студентов-психологов   превосходит   группу   студентов-физиков по уровню невербального интеллекта.

В соответствии со следующим шагом алгоритма определяем эмпирическую величину U:

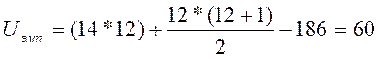
Поскольку в нашем случае n1  не  равно n2 подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу соответствующее ей пх:

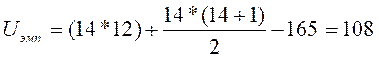
Такую проверку рекомендуется производить в некоторых руководствах (Рунион Р., 1982; Greene J., D'Olivera M., 1989). Для сопоставления с критическим значением выбираем меньшую величину U: Uэмп =60.

По Табл. II Приложения 1 определяем критические значения для соответствующих п, причем меньшее п принимаем за n1 (n1 = 12) и отыскиваем его в верхней строке Табл. II Приложения 1, большее n принимаем за п2 (п2 = 14), и отыскиваем его в левом столбце Табл. II Приложения 1.

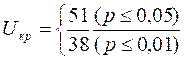
Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно,   мы   можем   констатировать   достоверные   различия,   если

Построим "ось значимости".

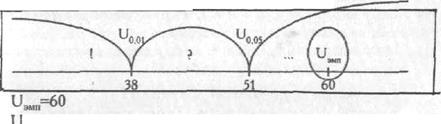
Uэмп >Uкр

 Ответ: Н0  принимается. Группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.

Обратим внимание на то, что для данного случая критерий Q Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значение невербального интеллекта приходится на группу физиков (см. Табл. 2.4).