Обоснование задачи сравнения распределений признака

Распределения могут различаться по средним, дисперсиям, асимметрии, эксцессу и по сочетаниям этих параметров. Рассмотрим несколько примеров.

На Рис. 4.1 представлены два распределения признака. Распределение 1 характеризуется меньшим диапазоном вариативности и меньшей дисперсией, чем распределение 2. В распределении 1 чаще встречаются значения признака, близкие к средней, а в распределении 2 чаще встречаются более высокие и более низкие, чем средняя, значения признака.

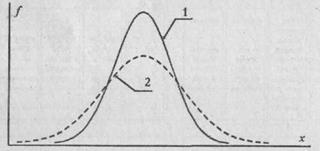
Рис 4.1. Кривые распределения признака с меньшим диапазоном вариативности признака (1) и большим диапазоном распределений признака (2): х - значения признака; ƒ - относительная частота их встречаемости

Именно такое соотношение может наблюдаться в распределении стенотипических признаков у мужчин (кривая 2) и женщин (кривая 1). Фенотипическая дисперсия мужского пола должна быть больше, чем женского (Геодакян В.А., 1974; 1993). Мужчины - это авангардная часть популяции, ответственная за поиск новых форм приспособления, поэтому у них чаще встречаются редкие крайние значения различных фенотипических признаков. Эти отклонения, по мнению В.А. Геодакяна, носят "футуристический" характер, это "пробы", включающие как будущие возможные пути эволюции, так и ошибки (Геодакян В.А., 1974, с. 381). В то же время женская часть популяции ответственна за сохранение уже накопленных изменений, поэтому у них чаще встречаются средние значения фенотипических признаков.

Анализ реально получаемых в исследованиях распределений может позволить нам подтвердить или опровергнуть данные теоретические предположения.

На Рис. 4.2 представлены два распределения, различающиеся по знаку асимметрии: распределение 1 характеризуется положительной асимметрией (левосторонней), а распределение 2 — отрицательной (правосторонней).

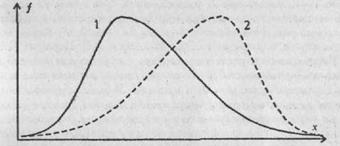
Рис. 4.2. Кривые распределения признака с положительной (левосторонней) асимметрией (1) и отрицательной (правосторонней) асимметрией (2); х - значения признаке;

ƒ -относительная частота их встречаемости

Данные кривые могут отражать распределение времени решения простой задачи (кривая 1) и трудной задачи (кривая 2). Простую задачу большинство испытуемых решают быстро, поэтому большая часть значений группируется слева. В то же время сама простота задачи может привести к тому, что некоторые испытуемые будут думать над нею очень, очень долго, дольше даже, чем над сложной. Трудную задачу большинство испытуемых решают в тенденция дольше, чем простую, но в то же время почти всегда находятся люди, которые решают ее мгновенно.

Если мы докажем, что распределения статистически достоверно различаются, это может стать основой для построения классификаций задач и типологий испытуемых. Например, мы можем выявлять испытуемых со стандартным соотношением признаков: простую задачу они решают быстро, а трудную - медленно, — и испытуемых с нестандартным соотношением: простую задачу решают медленно, а трудную - быстро и т.п. Далее мы можем сравнить выявленные группы испытуемых по показателям мотивации достижения, так как известно, что лица с преобладанием стремления к успеху предпочитают задачи средней трудности, где вероятность успеха примерно 0.5, а лица с преобладанием стремления избегать неудачи предпочитают либо очень легкие, либо, наоборот, очень трудные задачи (McClelland D.C., Winter D.G., 1969). Таким образом, и здесь сопоставление форм распределения может дать начало научному поиску.

Часто нам бывает полезно также сопоставить полученное эмпирическое распределение с теоретическим распределением. Например, для того, чтобы доказать, что оно подчиняется или, наоборот, не подчиняется нормальному закону распределения. Это лучше делать с помощью машинных программ обработки данных, особенно при больших объемах выборок. Подробные программы машинной обработки можно найти, например, в руководстве Э.В. Ивантер и Л.В. Коросова (1992).

В практических целях эмпирические распределения должны проверяться на "нормальность" в тех случаях, когда мы намерены использовать параметрические методы и критерии. В данном руководстве это относится лишь к методам дисперсионного анализа, поэтому способы проверки совпадения эмпирического распределения с нормальным описаны в Лекции 8, посвященной однофакторному дисперсионному анализу.

Традиционные для отечественной математической статистики критерии определения расхождения или согласия распределений - это метод χ2 К. Пирсона и критерий λ Колмогорова-Смирнова.

Оба эти метода требуют тщательной группировки данных и довольно сложных вычислений. Кроме того, возможности этих критериев в полной мере проявляются на больших выборках (n≥30). Тем не менее, они могут оказаться столь незаменимыми, что исследователю придется пренебречь экономией времени и усилий.

Например, они незаменимы в следующих двух случаях:

1)  в задачах, требующих доказательства неслучайности предпочтений в выборе из нескольких альтернатив;

2)  в задачах, требующих обнаружения точки максимального расхождения между двумя распределениями, которая затем используется для перегруппировки данных с целью применения критерия φ* (углового преобразования Фишера).

Рассмотрим вначале традиционные методы определения расхождения распределений, а затем возможности использования критерия φ* Фишера.