χ2  - критерий Пирсона

Назначения критерия

Критерий χ2 применяется в двух целях;

1)  для сопоставления эмпирического распределения признака с теоретическим - равномерным, нормальным или каким-то иным;

2)  для сопоставления двух, трех или более эмпирических распределений одного и того же признака1.

 На самом деле области применения критерия %2 многообразны, но в данном руководстве мы ограничиваемся только этими двумя, наиболее часто встречающимися на практике, целями.

Описание критерия

Критерий χ2 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.

Преимущество метода состоит в том, что он позволяет сопоставлять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтернативного распределения "да - нет", "допустил брак - не допустил брака", "решил задачу - не решил задачу" и т. п. мы уже можем применить критерий χ2.

Допустим, некий наблюдатель фиксирует количество пешеходов, выбравших правую или левую из двух симметричных дорожек на пути из точки А в точку Б (см. Рис. 4.3).

Рис. 4.3. Иллюстрация к примеру о теоретически равновероятном выборе из двух альтернатив - правой и левой дорожек, ведущих из точки А в точку Б

Допустим, в результате 70 наблюдений установлено, что 51 человек выбрали правую дорожку, и лишь 19 - левую. С помощью критерия χ2 мы можем определить, отличается ли данное распределение выборов от равномерного распределения, при котором обе дорожки выбирались бы с одинаковой частотой. Это вариант сопоставления полученного эмпирического распределения с теоретическим. Такая задача может стоять, например, в прикладных психологических исследованиях, связанных с проектированием в архитектуре, системах сообщения и др.

Но представим себе, что наблюдатель решает совершенно другую задачу: он занят проблемами билатерального регулирования. Совпадение полученного распределения с равномерным его интересует гораздо в меньшей степени, чем совпадение или несовпадение его данных с данными других исследователей. Ему известно, что люди с преобладанием правой ноги склонны делать круг против часовой стрелки, а люди с преобладанием левой ноги - круг по ходу часовой стрелки, и что в исследовании коллег2 преобладание левой ноги было обнаружено у 26 человек из 100 обследованных.

С помощью метода χ2 он может сопоставить два эмпирических распределения: соотношение 51:19 в собственной выборке и соотношение 74:26 в выборке других исследователей.

Это вариант сопоставления двух эмпирических распределений по простейшему альтернативному признаку (конечно, простейшему с математической точки зрения, а отнюдь не психологической).

Диалогичным образом мы можем сопоставлять распределения выборов из трех и более альтернатив. Например, если в выборке из 50 человек 30 выбрали ответ (а), 15 человек - ответ (б) и 5 человек - ответ (в), то мы можем с помощью метода χ2 проверить, отличается ли это распределение от равномерного распределения или от распределения ответов в другой выборке, где ответ (а) выбрали 10 человек, ответ (б) -25 человек, ответ (в) - 15 человек.

В тех случаях, если признак измеряется количественно, скажем, в баллах, секундах или миллиметрах, нам, быть может, придется объединить все обилие значений признака в несколько разрядов. Например, если время решения задачи варьирует от 10 до 300 секунд, то мы можем ввести 10 или 5 разрядов, в зависимости от объема выборки. Например, это будут разряды: 0-50 секунд; 51-100 секунд; 101-150 секунд и т. д. Затем мы с помощью метода χ2 будем сопоставлять частоты встречаемости разных разрядов признака, но в остальном принципиальная схема не меняется.

При сопоставлении эмпирического распределения с теоретическим мы определяем степень расхождения между эмпирическими и теоретическими частотами.

При сопоставлении двух эмпирических распределений мы определяем степень расхождения между эмпирическими частотами и теоретическими частотами, которые наблюдались бы в случае совпадения двух этих эмпирических распределений. Формулы расчета теоретических частот будут специально даны для каждого варианта сопоставлений.

Чем больше расхождение между двумя сопоставляемыми распределениями, тем больше эмпирическое значение χ2.

Гипотезы

Возможны несколько вариантов гипотез, в зависимости от задач, которые мы перед собой ставим.

Первый вариант:

H0: Полученное эмпирическое распределение признака не отличается от теоретического (например, равномерного) распределения.

H1: Полученное эмпирическое распределение признака отличается от теоретического распределения.

Второй вариант:

H0: Эмпирическое распределение 1 не отличается от эмпирического распределения 2.

Н1: Эмпирическое распределение 1 отличается от эмпирического распределения 2.

Третий вариант:

H0: Эмпирические распределения 1, 2, 3, ... не различаются между собой.

H1: Эмпирические распределения 1, 2, 3, ... различаются между собой.

Критерий χ2 позволяет проверить все три варианта гипотез.

Графическое представление критерия

Проиллюстрируем пример с выбором правой или левой дорожек на пути из точки А в точку Б. На Рис. 4.4 частота выбора левой дорожки представлена левым столбиком, а частота выбора правой дорожки - правым столбиком гистограммы. На оси ординат отмеряются относительные частоты выбора, то есть частоты выбора той или иной дорожки, отнесенные к общему количеству наблюдений. Для левой дорожки относительная частота, которая называется также частостью, составляет 19/70, то есть 0,27, а для правой дорожки 51/70, то есть 0.73.

Гистограмма - это диаграмма, в которой различная величина частот изображается различной высотой столбиков (Плохинский Н. А., 1970, с. 14.)

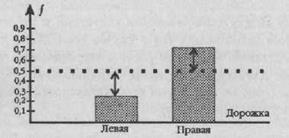
Рис. 4.4. Частоты выбора левой и правой дорожек; теоретическая частота представлена в виде горизонтальной планки, стрелками обозначены области расхождения между эмпирическими и теоретическими частотами

Если бы обе дорожки выбирались равновероятно, то половина испытуемых выбрала бы правую дорожку, а половина - левую. Вероятность выбора каждой из дорожек составляла бы 0,50.

Мы видим, что отклонения эмпирических частот от этой величины довольно значительны. Возможно, различия между эмпирическим и теоретическим распределением окажутся достоверными.

На Рис. 4.5 фактически представлены две гистограммы, но столбики сгруппированы так, что слева сопоставляются частоты предпочтения левой дорожки в выборе нашего наблюдателя (1) и в выборке Т.А. Доброхотовой и Н.Н. Брагиной (2), а справа - частоты предпочтения правой дорожки в этих же двух выборках.

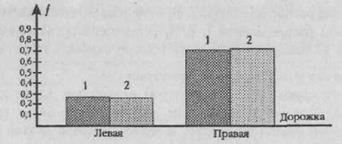
Рис. 4.5. Частоты выбора левой и правой дорожек в двух выборках испытуемых

1— Выборка наблюдателя;

2— Выборка других исследователей

Мы видим, что расхождения между выборками очень незначительны. Критерий χ2 скорее всего, подтвердит совпадение двух распределений.

Ограничения критерия

1. Объем выборки должен быть достаточно большим: n>50. При n<30 критерий χ2 дает весьма приближенные значения. Точность критерия повышается при больших п.

2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f>5. Это означает, что если число разрядов задано заранее и не может быть изменено, то мы не можем применять метод χ2, не накопив определенного минимального числа наблюдений. Если, например, мы хотим проверить наши предположения о том, что частота обращений в телефонную службу Доверия неравномерно распределяются по 7 дням недели, то нам потребуется 5*7=35 обращений. Таким образом, если количество разрядов (k) задано заранее, как в данном случае, минимальное число наблюдений (nmin) определяется по формуле: nmin = k*5.

3. Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях.

4. Необходимо вносить "поправку на непрерывность" при сопоставлении распределений признаков, которые принимают всего 2 значения.
При внесении поправки значение χ2 уменьшается (см. Пример с поправкой на непрерывность).

5. Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду.

Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений.

Правомерен вопрос о том, что считать числом наблюдений - количество выборов, реакций, действий или количество испытуемых, которые совершают выбор, проявляют реакции или производят действия. Если испытуемый проявляет несколько реакций, и все они регистрируются, то количество испытуемых не будет совпадать с количеством реакций. Мы можем просуммировать реакции каждого испытуемого, как, например, это делается в методике Хекхаузена для исследования мотивации достижения или в Тесте фрустрационной толерантности С. Розенцаейга, и сравнивать распределения индивидуальных сумм реакций в нескольких выборках.

В этом случае числом наблюдений будет количество испытуемых. Если же мы подсчитываем частоту реакций определенного типа в целом по выборке, то получаем распределение реакций разного типа, и в этом случае количеством наблюдений будет общее количество зарегистрированных реакций, а не количество испытуемых.

С математической точки зрения правило независимости разрядов соблюдается в обоих случаях: одно наблюдение относится к одному и только одному разряду распределения.

Можно представить себе и такой вариант исследования, где мы изучаем распределение выборов одного испытуемого. В когнитивно-бихевиоральной терапии, например, клиенту предлагается всякий раз фиксировать точной время появления нежелательной реакции, например, приступов страха, депрессии, вспышек гнева, самоуничижающих мыслей и т. п. В дальнейшем психотерапевт анализирует полученные данные, выявляя часы, в которые неблагоприятные симптомы проявляются чаще, и помогает клиенту строить индивидуальную программу предупреждения неблагоприятных реакций.

Можно ли с помощью критерия χ2 доказать, что некоторые часы являются в этом индивидуальном распределении более часто встречающимися, а другие - менее часто встречающимися? Все наблюдения - зависимы, так как они относятся к одному и тому же испытуемому; в то же время все разряды - неперекрещивающиеся, так как одни и тот же приступ относится к одному и только одному разряду (в данном случае - часу дня). По-видимому, применение метода χ2 будет в данном случае некоторым упрощением. Приступы страха, гнева или депрессии могут наступать неоднократно в течение дня, и может оказаться так, что, скажем, ранний утренний, 6-часовой, и поздний вечерний, 12-часовой, приступы обычно появляются вместе, а один и тот же день: в то же время дневной 3-часовой приступ появляется не ранее как через сутки после предыдущего приступа и не менее чем за двое суток до следующего и т. п. По-видимому, речь здесь может идти о сложной математической модели или вообще о чем-то таком, чего нельзя "поверить алгеброй". И тем не менее в практических целях может оказаться полезным использовать критерий для того, чтобы выявить систематическую неравномерность наступления каких-либо значимых событий, выбора, предпочтений и т. п. у одного и того же человека.

Итак, одно и то же наблюдение должно относиться только к одному разряду. Но считать ли наблюдением каждого испытуемого или каждую исследуемую реакцию испытуемого - вопрос, решение которого зависит от целей исследования (см., напр.,Ганзен В.А., Балин В.Д-. 1991, с.10).

Главное же "ограничение" критерия χ2 – то, что но кажется большинству исследователей пугающе сложным.

Попытаемся преодолеть миф о непостижимой трудности критерия χ2. Чтобы оживить изложение, рассмотрим шутливый литературный пример.

Шутливый пример

В гениальной комедии Н. В. Гоголя "Женитьба" у купеческой дочери Агафьи Тихоновны было пятеро женихов. Одного она сразу исключила из рассмотрения, потому что он был купеческого звания, как и она сама. А из остальных она не знала, кого выбрать: "Уж как трудно решиться, так просто рассказать нельзя, как трудно. Если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности, какая у Балтазара Балтазарыча, да, пожалуй, прибавить к этому еще дородности Ивана Павловича, я бы тогда тотчас решилась. А теперь поди подумай! просто голова даже стала болеть. Я думаю, лучше всего кинуть жребий" (Гоголь Н.В., 1959, с. 487). И вот Агафья Тихоновна положила бумажки с четырьмя именами в ридикюль, пошарила рукою в ридикюле и вынула вместо одного — всех!

Ей хотелось, чтобы жених совмещал в себе достоинства всех четверых, и, вынимая все бумажки вместо одной, она бессознательно совершала процедуру выведения средней величины. Но вывести среднюю величину из четверых людей невозможно, и Агафья Тихоновна в смятении. Она влюблена, но не знает, в кого. "Такое несчастное положение девицы, особливо еще влюбленной" (там же, с. 487).

Вся беда в том, что ни Агафья Тихоновна, ни ее тетушка, ни сваха Фекла Ивановна не были знакомы с критерием χ2 ! Именно он мог бы им помочь в решении их проблемы. С его помощью можно было бы попробовать установить, в кого больше влюблена Агафья Тихоновна. Но для этого нам не нужно измерять губы Никанора Ивановича или нос Ивана Кузьмича, или объем талии дородного экзекутора Ивана Павловича; не нужно нам и пускаться на какие-нибудь опасные эксперименты, чтобы определить, насколько далеко простирается развязность Балтазара Балтазарыча. Мы эти их достоинства принимаем как данность потому лишь, что они нравятся Агафье Тихоновне. Мы принимаем их за разряды одного и того же признака, например, направленности взгляда Агафьи Тихоновны: сколько раз она взглянула на губы Никанора Ивановича? На нос Ивана Кузьмича? Благосклонно взирала на дородного Ивана Павловича или развязного Балтазара Балтазаровича? Внимательная сваха или тетушка вполне могла бы этот признак наблюдать. Допустим, за полчаса смотрин ею зафиксированы следующие наблюдения.

Агафья Тихоновна:

сидела с опущенными глазами               25 минут;

благосклонно смотрела на Никанора Ивановича           14 раз;

благосклонно смотрела на Ивана Кузьмича        5 раз;

благосклонно смотрела на Ивана Павловича      8 раз;

благосклонно смотрела на Балтазара Балтазарыча          5 раз.

Представим это в виде таблицы.

 

Таблица 4.1

Распределение взгляда Агафьи Тихоновны между 4 женихами

Женихи	Никанор Иванович	Иван Кузьмич	Иван Павлович	Балтазар Балтазарыч	Всего взглядов
Количество взглядов	14	5	8	5	32

Теперь нам нужно сопоставить полученные эмпирические частоты с теоретическими. Если Агафья Тихоновна никому не отдает предпочтения, то данное распределение показателя направленности ее взгляда не будет отличаться от равномерного распределения: она на всех смотрит примерно с одинаковой частотой. Но если достоинства одного из женихов чаще притягивают ее взор, то это может быть основанием для матримониального решения.

Гипотезы

Н0: Распределение взглядов Агафьи Тихоновны между женихами не отличается от равномерного распределения.

H1: Распределение взглядов Агафьи Тихоновны между женихами отличается от равномерного распределения.

Теперь нам нужно определить теоретическую частоту взгляда при равномерном распределении. Если бы все взгляды невесты распределялись равномерно между 4-мя женихами, то, по-видимому, каждый из них получил бы по ¼ всех её  взглядов.

Переведем эти рассуждения на более формализованный язык. Теоретическая частота при сопоставлении эмпирического распределения с равномерным определяется по формуле:

4Все приведенные эмпирические частоты на самом деле пропорциональны количеству благосклонных высказываний невесты о женихах в тексте пьесы.

 

где n - количество наблюдений;

k - количество разрядов признака.

В нашем случае признак - взгляд невесты, направленный на кого-либо из женихов; количество разрядов признака - 4 направления взгляда, по количеству женихов; количество наблюдений - 32.

Итак, в нашем случае:

Теперь мы будем сравнивать с этой теоретической частотой все эмпирические частоты.

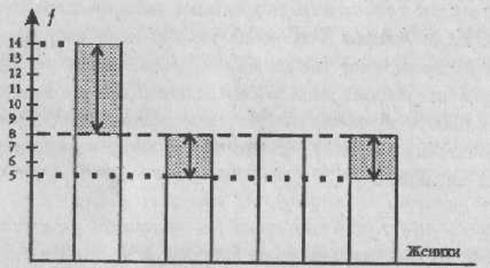
Никанор        Иван            Иван           Балтазар

Иванович      Кузьмич       Павлович    Балтазарыч

Рис. 4.6. Сопоставление эмпирических частот взгляда Агафьи Тихоновны на каждого из женихов (столбики гистограммы) с теоретической частотой {горизонтальная планка); темной штриховкой отмечены области расхождений между эмпирическими и теоретическими частотами

На Рис. 4.6 сопоставления эмпирических частот с теоретической представлены графически. Похоже, что области расхождений достаточно значительны, и Никанор Иванович явно опережает других женихов. Иван Павлович еще может на что-то надеяться, но для Ивана Кузьмича и Балтазара Балтазарыча отставка, по-видимому, неизбежна.

Однако для того, чтобы доказать неравномерность полученного эмпирического распределения, нам необходимо произвести точные расчеты. В методе χ2 они производятся с точностью до сотых, а иногда и до тысячных долей единицы.

Расчеты будем производить в таблице по алгоритму.

АЛГОРИТМ 13

Расчет критерия χ2

1.Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2.  Рядом с каждой эмпирической частотой записать теоретическую частоту (второй столбец).

3. Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле:

ν=k-1

где k - количество разрядов признака.

Если ν=l, внести поправку на "непрерывность".

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую часто ту и записать результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обозначить как χ2 эмп

8. Определить по Табл. IX Приложения 1 критические значения для данного числа степеней свободы V.

  Если χ2 эмп  меньше критического значения, расхождения между распределениями статистически недостоверны.

Если  χ2 эмп критическому значению или превышает его, расхождения между распределениями статистически достоверны.

Все вычисления для данного случая отражены в Табл. 4.2.

 

 

 

 

 

Таблица 4.2

Расчет критерия χ2 эмп при сопоставлении эмпирического

распределения взгляда Агафьи Тихоновны между женихами с равномерным распределением

Разряды-женихи		Эмпирическая частота взгляда (f’эj)	Теоретическая частота (fт)	(f’эj - fт)	(f’эj -fт)2	(f’эj -fт)/ƒт
1	Никанор Иванович	14	8	+6	36	4,500
2	Иван Кузьмич	5	8	-3	9	1,125
3	Иван Павлович	8	8	0	0	0
4	Балтазар Балтазарович	5	8	-3	9	1,125
	Суммы	32	32	0		6,750

Может показаться, что удобнее суммировать все возведенные в квадрат разности между эмпирическими и теоретическими частотами, а затем уже эту сумму разделить на ƒт. В данном случае это возможно, так как ƒт для всех разрядов одинакова. Однако позже мы увидим, что так бывает далеко не всегда. Нужно быть внимательными или, экономя свое внимание, просто взять за правило всякий раз вычислять (ƒэi – ƒт)2 /ƒт  до   суммирования.

Необходимо также всякий раз убеждаться в том, что сумма разностей между эмпирическими и теоретической частотами (сумма по третьему столбцу) равна 0. Если это равенство не соблюдается, это означает, что в подсчете частот или разностей допущена ошибка. Необходимо найти и устранить её прежде чем переходить к дальнейшим расчетам.

Алгоритм вычислений, таким образом, выражается формулой:

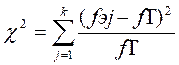
где fэj - эмпирическая частота по j-тому разряду признака; ƒт - теоретическая частота;

j - порядковый номер разряда;

k - количество разрядов признака.

В данном случае:

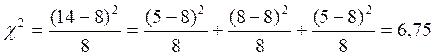
Для того, чтобы установить критические значения χ2 , нам нужно определить число степеней свободы ν по формуле:

v=k-l

где k - количество разрядов.

В нашем случае ν=4-l=3.

По Табл. IX Приложения 1 определяем:

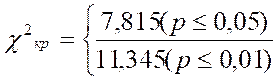
Построим "ось значимости". Ясно, что чем больше отклонения эмпирических частот от теоретической, тем больше будет величина χ2. Поэтому зона значимости располагается справа, а зона незначимости - слева.

К сожалению, на основании этих данных тетушка не сможет дать Агафье Тихоновне обоснованного ответа:

Χ2эмп < χ2кр.

 

Ответ: Но принимается. Распределение взгляда Агафьи Тихоновны между женихами не отличается от равномерного распределения.

Но, допустим, тетушка на этом не успокоилась. Она стала внимательно следить за тем, сколько раз племянница упомянет в разговоре каждого из женихов. Допустим, ею получено следующее распределение упоминаний Агафьей Тихоновной женихов и их достоинств:

Никанор Иванович -     15 раз,

Иван Кузьмич -         6 раз,

Иван Павлович -       9 раз,

Балтазар Балтазарыч -    6 раз.

Тетушка уже видит, что, похоже, Никанор Иванович ("уж такой деликатный, а губы, мать моя, - малина, совсем малина") пользуется большей благосклонностью Агафьи Тихоновны, чем все остальные женихи. У нее есть два пути, чтобы это доказать статистически.

1) Суммировать все проявления благосклонности со стороны невесты: взгляды + упоминания в разговоре, - и сопоставить полученное распределение с равномерным. Поскольку количество наблюдений возросло, есть шанс, что различия окажутся достоверными.

2) Сопоставить два эмпирических распределения - взгляда и упоминаний в разговоре, - с тем, чтобы показать, что они совпадают между собой, то есть и во взглядах, и в словах Агафья Тихоновна придерживается одинаковой системы предпочтений.

Проанализируем оба варианта сопоставлений.

В первом случае мы будем решать уже известную нам задачу сопоставления эмпирического распределения с теоретическим. Во втором случае мы будем сопоставлять два эмпирических распределения.

Первый вариант развития шутливого примера: увеличение количества наблюдений

Вначале создадим таблицу эмпирических частот, в которой будут суммированы все замеченные проявления благосклонности невесты.

Таблица 4.3

Распределение проявлений благосклонности невесты между женихами

Женихи	Никанор Иванович	Иван Кузьмич	Иван Павлович	Балтазар Балтазарыч	Всего
Количество проявлений	29	11	17	11	68

Теперь сформулируем гипотезы.

Н0: Распределение проявлений благосклонности невесты (взгляды и упоминания в разговоре) не отличается от равномерного распределения.

Н1: Распределение проявлений благосклонности невесты отличается от равномерного распределения.

Все расчеты произведем в таблице по алгоритму.

Таблица 4.4

Расчет критерия X2 при сопоставлении проявлений благосклонности Агафьи Тихоновны с равномерным распределением

Разряды-женихи		Эмпирическая частота взгляда (f’эj)	Теоретическая частота (fт)	(f’эj - fт)	(f’эj -fт)2	(f’эj -fт)/ƒт
1	Никанор Иванович	29	17	12	144	8,47
2	Иван Кузьмич	11	17	-6	36	2,12
3	Иван Павлович	17	17	0	0	0
4	Балтазар Балтазарович	11	17	-6	36	2,12
	Суммы	68	68	0		12,71

ƒт=n/k=68/4=17

v=k-l=3

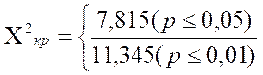
Х2 эмп = 12,71
      Х2 эмп >Х2 кр.

Ответ: Но отклоняется, принимается Н1. Распределение проявлений благосклонности невесты между женихами отличается от равномерного распределения (р<0,01).

На этом примере мы убедились, что увеличение числа наблюдений повышает достоверность результата, если, конечно, в новых наблюдениях воспроизводится прежняя тенденция различий.

Второй вариант развития шутливого примера: сопоставление двух эмпирических распределений

Теперь мы должны ответить на вопрос, одинаковая ли система предпочтений проявляется во взгляде Агафьи Тихоновны и ее словах?

Сформулируем гипотезы.

H0: Распределения невербально и вербально выражаемых предпочтений не различаются между собой.

H1: Распределения невербально и вербально выражаемых предпочтений различаются между собой.

Для подсчета теоретических частот нам теперь придется составить специальную таблицу (Табл. 4.5). Ячейки в двух столбцах слева обозначим буквами. Для каждой из них теперь будет подсчитана особая, только к данной ячейке относящаяся, теоретическая частота. Это обусловлено тем, что количества взглядов и словесных отзывов невесты о женихах неравны; взглядов 32, а словесных отзывов - 36. Мы должны всякий раз учитывать эту пропорцию.

 

 

Таблица 4.5

Эмпирические и теоретические частоты взглядов и упоминаний о женихах

Разряды-женихи		Эмпирические частоты		Суммы	Теоретические частоты
		Взгляда	Упоминаний в разговоре		Взгляда	Упоминаний в разговоре
1	Ник.Ив.	14   А	15  Б	29	13,63  А	15,37  Б
2	Ив.Куз.	5    В	6   Г	11	5,17   В	5,83    Г
3	Ив.Павл.	8   Д	9   Е	17	7,99   Д	9,01   Е
4	Бал.Бал.	5   Ж	6  3	11	5,17   Ж	5,83   З
Суммы:		32	36	68	32	36

Рассчитаем эту пропорцию. Всего проявлений благосклонности отмечено 68, из них 32 - взгляды и 36 - словесные высказывания. Доля взглядов составит 32/68=0,47; доля упоминаний - 36/68=0,53.

Итак, во всех строках взгляды должны были бы составлять 0,47 всех проявлений по данной строке, а упоминания в разговоре - 0,53 всех проявлений. Теперь, зная суммы проявлений по каждой строке, мы можем рассчитать теоретические частоты для каждой ячейки

Табл. 4.5.

 

ƒА теор = 29*0,47=13,63

ƒБ теор = 29*0,53=15,37

ƒВ теор = 11*0,47=5,17

ƒГ теор = 11*0,53=5,83

ƒД теор = 17*0,47=7,99

ƒЕ теор = 17*0,53=9,01

ƒЖ теор = 11*0,47=5,17

ƒЗ теор = 11*0,53=5,83

Ясно, что сумма теоретических частот по строкам будет равняться сумме всех проявлений по данной строке. Например,

ƒА теор +  ƒБ теор =13,63+15,37=29

ƒВ теор + ƒГ теор =5,17+5,83=11

ƒД теор + ƒЕ теор =7,99+9,01=17 и.т.д.

При такого рода подсчетах лучше всякий раз себя проверить. Теперь мы можем вывести общую формулу подсчета ƒтеор для сопоставления двух или более эмпирических распределений:

ƒтеор =                     (Сумма частот по         *         (Сумма частот по

                           соответствующей строке)      соответствующему столбцу)

                                        (Общее количество наблюдений)

 

Соответствующими строкой и столбцом будут та строка и тот столбец, на пересечении которых находится данная ячейка таблицы. Теперь нам лучше всего сделать развертку Табл. 4.5, представив все ячейки от А до Ж в виде первого столбца - это будет столбец эмпирических частот. Вторым столбцом будут записаны теоретические частоты. Далее будем действовать по уже известному алгоритму. В третьем столбце будет представлены разности эмпирических и теоретических частот, в четвертом - квадраты этих разностей, а в пятом - результаты деления этих квадратов разностей на соответствующие каждой строке теоретические частоты. Сумма в нижнем правом углу таблицы и будет представлять собой эмпирическую величину χ2 (Табл. 4.6).

Таблица 4.6

Расчет критерия χ2 при сопоставлении распределений невербальных и вербальных признаков благосклонности невесты

Ячейки таблицы частот		Эмпирическая частота  (f’эj)	Теоретическая частота (fт)	(f’эj - fт)	(f’эj -fт)2			(f’эj -fт)/ƒт
1	А	14	13,63	+0,37		0,14	0,01
2	Б	15	15,37	-0,37		0,14	0,01
3	В	5	5,17	-0,17		0,03	0,01
4	Г	6	5,83	+0,17		0,02	0,00
5	Д	8	7,99	+0,01		0,00	0,00
6	Е	9	9,01	-0,01		0,00	0,00
7	Ж	5	5,17	-0,17		0,03	0,01
8	З	6	5,83	+0,17		0,02	0,00
	Суммы	68	68	0			0,04

Число степеней свободы при сопоставлении двух эмпирических распределений определяется по формуле:

v=(k-l)*(c-l),

где k - количество разрядов признака (строк в таблице эмпирических частот);

с - количество сравниваемых распределений (столбцов в таблице эмпирических частот).

В данном случае таблицей эмпирических частот является левая, эмпирическая часть таблицы 4.5, а не на ее развертка (Табл. 4.6).

Количество разрядов - это количество женихов, поэтому k=4.

 Количество сопоставляемых распределений с=2.

Итак, для данного случая,

v=(4-l)*(2-l)=3

Определяем по Табл. IX Приложения 1 критические значения

Для ν=3:

 

 

 

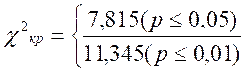
χ2эмп=0,04

χ2  < χ2  кр

 

Ответ: Но принимается. Распределения невербально и вербально выражаемых невестой предпочтений не различаются между собой.

Итак, Агафья Тихоновна весьма последовательна в проявлении своих предпочтений, хотя, по-видимому, сама этого пока не замечает.

Иллюстрация 2

 

Третий вариант развития шутливого примера: сопоставление встречных выборов

К сожалению, в этом пункте мы от комедии вынуждены перейти к драме - истинной драме любви. Ибо, судя по тексту пьесы, проявляемые женихами признаки влюбленности и симпатии по отношению к невесте отнюдь не соответствуют ее собственной системе предпочтений. У Ивана Павловича, а, главное, у Никанора Ивановича, которому невестой отдается столь явное предпочтение, проскальзывают в разговоре по большей части как раз отрицательные и задумчиво-неодобрительные отзывы о невесте: "Нос велик... Нет, не то. Не то... Я даже думаю, что вряд ли она знакома с обхождением высшего общества. Да и знает ли она еще по-французски".

Благосклонных отзывов ("А сказать правду - мне понравилась она потому, что полная женщина" и т. п.) поступило:

от Никанора Ивановича - ни одного;

от Ивана Кузьмича -15;

от Ивана Павловича – 6;

от Балтазара Балтазарыча - 18.

Попробуем ответить на вопрос: согласуются ли распределения благосклонных отзывов невесты о женихах и женихов о невесте?

Мы видим, что это действительно особая задача. Мы сопоставляем два эмпирических распределения с совпадающей классификацией разрядов, но в одном случае это распределение реакций одного человека на четверых других, а в другом случае это реакции четырех человек на одного и того же человека.

Такая модель взаимных реакций может использоваться отнюдь не только в области брачных консультаций, но ив решении задач "построения команды", выбора заместителя, подбора пар в тех видах деятельности, где требуется активное постоянное взаимодействие, в исследованиях социальной перцепции и взаимного влияния, в тренинге сенситивности и др.

Сформулируем гипотезы.

Н0: Распределение положительных отзывов невесты совпадает с распределением положительных отзывов женихов.

H1: Распределение положительных отзывов невесты не совпадает с распределением положительных отзывов женихов.

Построим таблицу для подсчета теоретических частот.

 

 

 

 

 

 

Таблица 4.7

Эмпирические и теоретические частоты положительных высказываний невесты о женихах и женихов о невесте

Разряды-женихи		Эмпирические частоты		Суммы	Теоретические частоты
		Положительных высказываний невесты о женихах	Положительных высказываний женихов о невесте		Положительных высказываний невесты о женихах	Положительных высказываний женихов о невесте
1	Ник.Ив.	15   А	0  Б	15	7,20  А	7,80  Б
2	Ив.Куз.	6    В	15   Г	21	10,08   В	10,92   Г
3	Ив.Павл.	9   Д	6  Е	15	7,20  Д	7,80  Е
4	Бал.Бал.	6   Ж	18  3	24	11,52  Ж	12,48   З
Суммы:		36	39	75	36	39

Теоретические частоты рассчитываем по уже известной формуле:

ƒтеор =                     (Сумма частот по         *         (Сумма частот по

                           соответствующей строке)      соответствующему столбцу)

                                        (Общее количество наблюдений)

ƒА теор = 15*36/75=7,20

ƒБ теор = 15*39/75=7,80

ƒВ теор = 21*36/75=10,08

ƒГ теор = 21*39/75=10,92

ƒД теор = 15*36/75=7,20

ƒЕ теор = 15*39/75=7,80

ƒЖ теор = 24*36/75=11,52

ƒЗ теор =  24*39/75=12,48

Суммы теоретических частот по строкам совпадают. Все дальнейшие расчеты выполним в таблице по алгоритму.

 

 

 

 

Таблица 4.8

Насчет критерия % при сопоставлении распределении высказывании невесты о женихах и женихов о невесте

Ячейки таблицы частот		Эмпирическая частота  (f’эj)	Теоретическая частота (fт)	(f’эj - fт)	(f’эj -fт)2			(f’эj -fт)/ƒт
1	А	15	7,20	+7,80		60,84	8,45
2	Б	0	7,80	-7,80		60,84	7,80
3	В	6	10,08	-4,08		16,65	1,65
4	Г	15	10,92	+4,08		16,65	1,52
5	Д	9	7,20	+1,80		3,24	0,45
6	Е	6	7,80	-1,80		3,24	0,42
7	Ж	6	11,52	-5,52		30,47	2,64
8	З	18	12,48	+5,52		30,47	2,44
	Суммы	75	75	0			25,37

Определим число степеней свободы ν по количеству строк k и

столбцов с в левой части Табл. 4.7: (k=4, c=2).

ν=(k-1)*(c-1)=3

Критические значения χ2 для ν =3 нам уже известны:

 

 

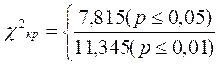
χ2эмп=25,37

χ2эмп >χ2кр

 

Omвem: H0 отвергается. Принимается Н1.

Распределение положительных отзывов предпочтений невесты не совпадает с распределением положительных отзывов женихов (р<0,01).

Итак, если бы Иван Кузьмич Подколесин не сбежал, Агафью Тихоновну могло бы ожидать не меньшее разочарование: предпочитаемый ею Никанор Иванович, "тонкого поведения человек", ее отвергает.

Мы не рассмотрели лишь третью группу возможных гипотез в методе χ2. Они, как мы помним, касаются сопоставлений одновременно 3 и более распределений. Принцип расчетов там такой же, как и при сопоставлении двух эмпирических распределений. Это касается и формулы расчета теоретических частот, и алгоритма последующих расчетов.

Рассмотрим особые случаи в применении метода χ2.

Особые случав в применении критерия

1. В случае, если число степеней свободы v=l, т. е. если признак принимает всего 2 значения, необходимо вносить поправку на непрерывность5.

2. Если признак варьирует в широком диапазоне (например, от 10 до 140 сек. и т.п.), возникает необходимость укрупнять разряды.

5 Поправка на непрерывность при V=l предназначена для корректировки несоответствия между дискретным биномиальным распределением и непрерывным рас- пределением (Рунион Р., 1982, с. 39.)

Особый случай 1: поправка на непрерывность для признаков, которые принимают всего 2 значения

Поправка на непрерывность вносится при следующих условиях:

а) когда эмпирическое распределение сопоставляется с равномерным распределением, и количество разрядов признака k=2, a v=k—1=1;

6) когда сопоставляются два эмпирических распределения, и количество разрядов признака равно 2, т.е. и количество строк k=2. и количество столбцов с=2, и v=(k—1)*(с—1)=1.

 

Вариант "а": поправка на непрерывность при сопоставлении эмпирического распределения с равномерным. Это тот случай сопоставлений, когда мы, говоря простым языком, проверяем, поровну ли распределились частоты между двумя значениями признака.

Пример с поправкой на непрерывность.

В исследовании порогов социального атома6 профессиональных психологов просили определить, с какой частотой встречаются в их записной книжке мужские и женские имена коллег-психологов. Попытаемся определить, - отличается ли распределение, полученное по записной книжке женщины-психолога X, от равномерного распределения. Эмпирические частоты представлены в Табл. 4.9

6 Социальный атом "... состоит из всех отношений между человеком и окружающими его людьми, которые в данный момент тем или иным образом с ним связаны" (Moreno J. L, 1951.)

Таблица 4.9

Эмпирические частоты встречаемости имен мужчин и женщин в записной книжке психолога X

Мужчин	Женщин	Всего человек
22	45	67

Сформулируем гипотезы.

H0: Распределение мужских и женских имен в записной книжке X не отличается от равномерного распределения.

H1: Распределение мужских и женских имен в записной книжке X отличается от равномерного распределения.

Количество наблюдений n=67;  количество значений признака k=2.

Рассчитаем теоретическую частоту: ƒтеор = n/k=33.5

Число степеней свободы v=k—1=1.

Далее все расчеты производим по известному алгоритму, но с одним добавлением: перед возведением в квадрат разности частот мы должны уменьшить абсолютную величину этой разности на 0,5 (см. Табл. 4.10, четвертый столбец).

 

 

 

Таблица 4.10

Расчет критерия χ2 при сопоставлении эмпирического распределения имен с теоретическим равномерным распределением

Разряды – принадлежность к тому или иному полу		Эмпирическая частота (ƒэj)	Теоретическая частота (ƒт)	(ƒэj-ƒт)	(ƒэj-ƒт-0.5)	(ƒэj-ƒт-0.5)2	(ƒэj-ƒт-0.5)2
							(ƒт)
1	Мужчины	22	33,5	-11,5	11	121	3,61
2	Женщины	45	33,5	+11,5	11	121	3,61
Суммы:		67	67	0			7,22

Для v=l определяем по Табл. IX Приложения 1 критические значения:

 

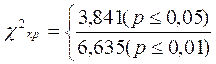
χ2эмп=7,22

χ2эмп >χ2кр

Ответ: Но отклоняется, принимается Н1. Распределение мужских и женских имен в записной книжке психолога X отличается от равномерного распределения (р<0,01).

 

Вариант "б": поправка на непрерывность при сопоставлении двух эмпирических распределений

Попытаемся определить, различаются ли распределения мужских и женских имен у психолога X и психолога С, тоже женщины. Эмпирические частоты приведены в Табл. 4.11.

 

 

 

 

 

Таблица 4.11

Эмпирические частоты встречаемости имен мужчин и женщин в записных книжках психолога X, и психолога С.

	Мужчин	Женщин	Всего человек
Психолог X. Психолог С.	22         А 59         В	45           Б 109         Г	67 168
Суммы	81	154	235

Сформулируем гипотезы. H0: Распределения мужских и женских имен в двух записных книжках не различаются.

H1: Распределения мужских и женских имен в двух записных книжках различаются между собой.      

Теоретические частоты рассчитываем по уже известной формуле:

ƒтеор =                     (Сумма частот по         *         (Сумма частот по

                           соответствующей строке)      соответствующему столбцу)

                                        (Общее количество наблюдений)

А именно, для разных ячеек таблицы эмпирических частот,

ƒА теор = 67*81/235=23,09

ƒБ теор = 67*154/235=43,91

ƒВ теор = 168*81/235=57,91

ƒГ теор = 168*154/235=110,09

Число степеней свободы v=(k—l)*(c—1)=1

Все дальнейшие расчеты проводим по алгоритму (Табл. 4.12)

Таблица 4.12

Расчет критерия при сопоставлении двух эмпирических распределений мужских и женских имен

Ячейки таблицы эмпирических частот		Эмпирическая частота (ƒэj)	Теоретическая частота (ƒт)	(ƒэj-ƒт)	(ƒэj-ƒт-0.5)	(ƒэj-ƒт-0.5)2	(ƒэj-ƒт-0.5)2
							(ƒт)
1	А	22	23,09	-1,09	0,59	0,35	0,015
2	Б	45	43,91	+1,09	0,59	0,35	0,008
3	В	59	57,91	+1,09	0,59	0,35	0,006
4	Г	109	110,09	-1,09	0,59	0,35	0,03
Суммы:		235	235,00	0			0,032

Критические значения χ2 при ν=1 нам известны по предыдущему примеру:

 

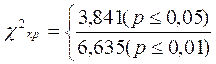
χ2эмп=0,03

χ2эмп < χ2кр

Ответ: H0 принимается. Распределения мужских и женских имен в записных книжка двух психологов совпадают.

Поправки на непрерывность и всех остальных подсчетов можно избежать, если использовать по отношению к подобного рода задачам метод ф* Фишера (см. параграф 5.4).

Особый случай 2; укрупнение разрядов признака, который варьирует в широкой диапазоне значений

Если признак варьирует в широком диапазоне значений, например, от 10 до 140 сек или от 0 до 100 мм и т. п., то вряд ли мы сможем принимать каждое значение признака за самостоятельный разряд: 10 сек, 11 сек, 12 сек и т. д. до 100 сек. Одно из ограничений критерия X2 состоит в том, что теоретически на каждый разряд должно приходиться не менее 5 наблюдений: ƒтеор >5. Если у признака 90 значений, и каждое из них принимается за самостоятельный разряд, то необходимо иметь не менее 5*90=450 наблюдений! Если же наблюдений меньше 450, то придется укрупнять разряды до тех пор, пока на каждый разряд не будет приходиться по 5 наблюдений. Это не означает, что в каждом разряде реально должно быть 5 наблюдений; это означает, что теоретически на каждый разряд их приходится по 5. Рассмотрим это на примере.

Пример с укрупнением разрядов признака

Тест Мюнстерберга для измерения избирательности перцептивного внимания в адаптированном варианте М.Д. Дворяшиной (1976) предъявлялся студентам факультета психологии Ленинградского университета (n1=156) и артистам балета Мариинского театра (n2=85). Материал методики состоит из бланка с набором букв русского алфавита, в случайном порядке перемежающихся. Среди этого фона скрыто 24 слова разной степени сложности: "факт", "хоккей", "любовь", "конкурс", "психиатрия" и т.п. Задача испытуемого возможно быстрее отыскать их и подчеркнуть (Дворяшина М.Д., 1976, с. 124). Совпадают ли распределения количества ошибок (пропусков слов) в двух выборках (Табл. 4.13)?

Таблица 4.13

Эмпирические частоты пропуска слов в тесте Мюнстерберга в двух выборках испытуемых (по данным М.Д. Дворяшиной, Е.В. Сидоренко, 1973)

Разряды		Эмпирические частоты пропусков слов
		В группе студентов (n1 =156)	В группе артистов балета (n2 =85)	Суммы
1	0 пропусков	93	22	115
11	1 пропуск	27	20	47
111	2 пропуска	11	16	27
1У	3 пропуска	15	4	19
У	4 пропуска	5	3	8
У1	5 пропусков	3	11	14
У11	6 пропусков	2	3	5
У111	7 пропусков	0	3	3
1Х	8 пропусков	0	2	2
Х	9 пропусков	0	1	1
Суммы		156	85	241

Сформулируем гипотезы.

H0: Распределения ошибок (пропусков слов) в выборках студентов и артистов балета не различаются между собой.

H1: Распределения ошибок (пропусков слов) в выборках студентов и артистов балета различаются между собой.

Прежде чем перейти к расчету теоретических частот, обратим внимание на последние 4 значения признака, от 6 пропусков и ниже. Очевидно, что ƒтеор для любой из ячеек последних 4 строк таблицы будет меньше 5. Например, для ячейки, отмеченной кружком:

ƒтеор =                     (Сумма частот по         *         (Сумма частот по

                           соответствующей строке)      соответствующему столбцу)

                                        (Общее количество наблюдений)

ƒтеор=5*85/241=1,763

Полученная теоретическая частота меньше 5.

Для того, чтобы решить, какие разряды нам следует укрупнить,
чтобы ƒтеор была не меньше 5, выведем формулу расчета минимальной суммы частот по строке по формуле: 

Минимальная           (ƒтеор минимальная)*(общее количество наблюдений)

сумма                  = ______________________________________________

по строке                   сумма частот по столбцу с наименьшим n

В данном случае столбцом с наименьшим количеством наблюдений является столбец, относящийся к выборке артистов балета (n=85).

Определим минимальную сумму частот для каждой строки:

 Минимальная сумма по строке =5*241/85=14,16

Мы видим, что для получения такой суммы нам недостаточно объединения последних 4 строк Табл. 4.13, так как сумма частот по ним меньше 14 (5+3+2+1=11), а нам необходима сумма частот, превышающая 14. Следовательно, придется объединять в один разряд пять нижних строк Табл. 4.13: теперь любое количество пропусков от 5 до 9 будет составлять один разряд.

Однако это еще не все. Мы видим, далее, что в строке "4 пропуска" сумма составляет всего 8. Значит, ее необходимо объединить со следующей строкой. Теперь и 3, и 4 пропуска будут входить в один разряд. Все остальные суммы по строкам больше 14, поэтому мы не нуждаемся в дальнейшем укрупнении разрядов.

Эмпирические частоты по укрупненным разрядам представлены в Табл. 4.14

Таблица 4.14

Эмпирические частоты пропуска слов по укрупненным разрядам в двух выборках испытуемых

Разряды		Эмпирические частоты пропуска слов				Суммы
		В группе студентов (n1=156)		В группе артистов (n2=85)
1	0 пропусков	93	А	22	Б	115
11	1 пропуск	27	В	20	Г	47
111	2 пропуска	11	Д	16	Е	27
1У	3-4 пропуска	20	Ж	7	З	27
У	5-9 пропусков	5	И	20	К	25
Суммы		156		85		241

Исследователю бывает огорчительно терять информацию, заведомо утрачиваемую при укрупнении разрядов. Например, в данном случае нас может интересовать, удалось ли сохранить специфический для второй выборки спад частот на 3 и 4 пропусках и резкий их подъем на 5 пропусках (Рис. 4.7).

Сравним графики на Рис. 4.7 и Рис. 4.8. Мы видим, что спад частот во второй выборке на 3-х и 4-х пропусках сохранился, а спад на 2-х пропусках в первой выборке стал еще более заметным. В то же время все возможные различия в частотах в диапазоне от 5-и до 9-и пропусков теперь оцениваются только глобально, по

Рис.4.7. Графики изменения эмпирических частот пропусков по «естественным»разрядам: а) в выборке студентов; б) в выборке артистов балета.

соотношению общих сумм частот в этих диапазонах. По графику на Рис. 4.8 мы уже не можем определить, какое максимальное количество пропусков встречается в первой группе и какое - во второй. Сопоставление распределений на этом конце становится более грубым.

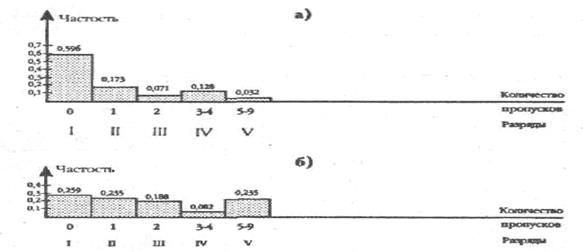
Рис. 4.8. Графики изменения эмпирических частот по укрупненным разрядам: а) в выборке студентов; 6) в выборке артистов балета

Если бы у нас было больше испытуемых в выборке артистов балета, то, возможно, удалось бы сохранить подъем частоты на 5-и пропусках. Сейчас же нам придется довольствоваться сопоставлением по данным укрупненным разрядам.

Перейдем к подсчету теоретических частот для каждой ячейки Табл. 4.14

ƒА теор = 115*156/241=74,44

ƒБ теор = 115*85/241=40,56

ƒВ теор = 47*156/241=30,41

ƒГ теор = 47*85/241=16,59

ƒД теор = 27*156/241=17,47

ƒЕ теор = 27*85/241=9,53

ƒЖ теор = 27*156/241=17,47

ƒЗ теор =  27*85/241=9,53

ƒИ теор    25*156/241=16,18

ƒК теор    25*85/241=8,82

Определим количество степеней свободы ν по формуле:

v=(k-l)*(c-l)

где k - количество строк (разрядов),

с - количество столбцов (выборок).

Для данного случая:

v=(5-l)*(2-l)=4

Все дальнейшие расчеты произведем в таблице по Алгоритму 13. Поправка на непрерывность не требуется, так как V>1.

Таблица 4.15

Расчет критерия X2 при сопоставлении двух эмпирических распределений пропусков слов в тесте Мюнстерберга (n1=156; n2 =85)

Ячейки таблицы частот		Эмпирическая частота  (f’эj)	Теоретическая частота (fт)	(f’эj - fт)	(f’эj -fт)2			(f’эj -fт)/ƒт
1	А	93	74,44	18,56		344,47	4,63
2	Б	22	46,56	-18,56		344,47	8,49
3	В	27	30,41	-3,41		11,63	0,38
4	Г	20	16,59	3,41		11,63	0,70
5	Д	11	17,47	-6,47		41,86	2,40
6	Е	16	9,53	6,47		41,86	4,40
7	Ж	20	17,47	2,53		6,401	0,37
8	З	7	9,53	-2,53		6,401	0,67
9	И	5	16,18	-11,18		124,99	7,72
10	К	20	8,82	11,18		124,99	14,17
	Суммы	241	241	0,00			43,95

По Табл. IX Приложения 1 определяем критические значения при ν=4:

 

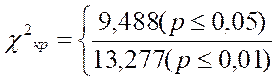
χ2эмп=43,95

χ2эмп > χ2кр

 

Ответ: Но отвергается. Принимается H1. Распределения пропусков слов в выборках студентов и артистов балета различаются между собой (р<0,01).

В распределении ошибок у артистов балета можно заметить два выраженных максимума (0 пропускав и 5 пропусков), что может указывать на два возможных источника ошибок7.

7Целесообразно было бы проверить совпадение распределения ошибок в обеих выборках с распределением Пуассона. Закону Пуассона подчиняются распределения редких событий, приходящихся 0, 1, 2,... раз на сотни и тысячи наблюдений. Однако в данном случае эта модель неприменима: средняя и дисперсия не равны друг другу и составляют, соответственно, 0,91 и 1,96 в первой выборке и 2,29 и 5,43 во второй выборке.