λ - критерий Колмогорова-Смирнова

Назначение критерия

Критерий λ предназначен для сопоставления двух распределений:

а)  эмпирического с теоретическим, например, равномерным или нормальным;

б) одного эмпирического распределения с другим эмпирическим распределением.

Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.

Описание критерия

Если в методе χ2 мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.

Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия λ  включается эта разность. Чем больше эмпирическое значение λ, тем более существенны различия.

Гипотезы                                                                -

Н0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).

H1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).

Графическое представление критерия

Рассмотрим для иллюстрации распределение желтого (№4) цвета в 8-цветном тесте М. Люшера. Если бы испытуемые случайным образом выбирали цвета, то желтый цвет, так же, как и все остальные, равновероятно мог бы занимать любую из 8-и позиции выбора. На практике, однако, большинство испытуемых помещают этот цвет, "цвет ожидания и надежды" на одну из первых позиций ряда.

На Рис. 4.9 столбиками представлены относительные частоты8 попадания желтого цвета сначала на 1-ю позицию (первый левый столбик), затем на 1-ю и 2-ю позицию (второй столбик), затем на 1-ю, 2-ю и 3-ю позиции и т. д. Мы видим, что высота столбиков постоянно возрастает, так как они отражают относительные частоты, накопленные к данной позиции. Например, столбик на 3-й позиции имеет высоту 0,51. Это означает, что на первые три позиции желтый цвет помещают 51% испытуемых.

8 Относительная частота, или частость, - это частота, отнесенная к общему количеству наблюдении; в данном случае это частота попадания желтого цвета на данную позицию, отнесенная к количеству испытуемых. Например, частота попадания желтого цвета на 1-ю позицию ƒ=24; количество испытуемых n=102; относительная частота ƒ*=ƒ/n=О,235.

Прерывистой линией на Рис. 4.9 соединены точки, отражающие накопленные частоты, которые наблюдались бы, если бы желтый цвет с равной вероятностью попадал на каждую из 8-и позиций. Сплошными линиями обозначены расхождения между эмпирическими и теоретическими относительными частотами. Эти расхождения обозначаются как d.

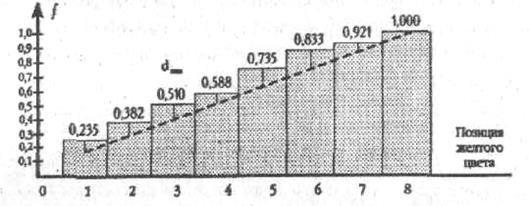
Рис 4.9. Сопоставления в критерии λ: стрелками отмечены расхождения между эмпирическими и теоретическими накоплениями относительными частотами по каждому разряду

Максимальное расхождение на Рис. 4.9 обозначено как dmax Именно эта, третья позиция цвета, и является переломной точкой, определяющей, достоверно ли отличается данное эмпирическое распределение от равномерного. Мы проверим это при рассмотрении Примера 1.

Ограничения критерия λ

1. Критерии требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо, чтобы n1,2 >50. Сопоставление эмпирического распределения с теоретическим иногда допускается при n>5 (Ван дер Варден Б.Л., 1960; Гублер Е.В., 1978).

2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение. Например, мы можем за разряды принять дни недели, 1-й, 2-й, 3-й месяцы после прохождения курса терапии, повышение температуры тела, усиление чувства недостаточности и т. д. В то же время, если мы возьмем разряды, которые случайно оказались выстроенными в данную последовательность, то и накопление частот будет отражать лишь этот элемент случайного соседства разрядов. Например, если шесть стимульных картин в методике Хекхаузена разным испытуемым предъявляются в разном порядке, мы не вправе говорить о накоплении реакций при переходе от картины №1 стандартного набора к картине №2 и т. д. Мы не можем говорить об однонаправленном изменении признака при сопоставлении категорий "очередность рождения", "национальность", "специфика полученного образования" и т.п. Эти данные представляют собой номинативные шкалы: в них нет никакого однозначного однонаправленного изменения признака.

Итак, мы не можем накапливать частоты по разрядам, которые отличаются лишь качественно и не представляют собой шкалы порядка. Во всех тех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, нам следует применять метод χ2 .

Пример 1: Сопоставление эмпирического распределения с теоретическим

В выборке здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19-ти до 22 лет, средний возраст 20 лет, проводился тест Люшера в 8-цветном варианте. Установлено, что желтый цвет предпочитается испытуемыми чаще, чем отвергается (Табл. 4.16). Можно ли утверждать, что распределение желтого цвета по 8-и позициям у здоровых испытуемых отличается от равномерного распределения?

Таблица 4.16

Эмпирические частоты попадания желтого цвета на каждую из 8 позиций (n=102)

Разряды	Позиции желтого цвета							Сумма
	1	2	3    4	5	6	7	8
Эмпирические частоты	24	25	13 | 8	15	10	9	8	102

Сформулируем гипотезы.

H0: Эмпирическое распределение желтого цвета по восьми позициям не отличается от равномерного распределения.

H1: Эмпирическое распределение желтого цвета по восьми позициям отличается от равномерного распределения.

Теперь приступим к расчетам, постепенно заполняя результатами таблицу расчета критерия λ. Все операции лучше прослеживать по Табл. 4.17, тогда они будут более понятными.

Занесем в таблицу наименования (номера) разрядов и соответствующие им эмпирические частоты (первый столбец Табл. 4.17).

Затем рассчитаем эмпирические частости ƒ* по формуле:

ƒ*j = ƒ*/n

где fj - частота попадания желтого цвета на данную позицию;      n - общее количество наблюдений;

      j - номер позиции по порядку.

Запишем результаты во второй столбец (см. Табл. 4.17).

Теперь нам нужно подсчитать накопленные эмпирические частости ∑ƒ*. Для этого будем суммировать эмпирические частости ƒ*. Например, для 1-го разряда накопленная эмпирическая частость будет равняться эмпирической частости 1-го разряда, Eƒ*1=0,2359 .

Для 2-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го и 2-го разрядов:

Eƒ*1+2=O,235+0,147=0,382

Для 3-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го, 2-го и 3-го разрядов:

Eƒ*1+2+3=0,235+0,147+0,128=0,510

Мы видим, что можно упростить задачу, суммируя накопленную эмпирическую частость предыдущего разряда с эмпирической частостью данного разряда, например, для 4-го разряда:

Eƒ*1+2+3+4=0,510+0,078=О,588

Запишем результаты этой работы в третий столбец.

Теперь нам необходимо сопоставить накопленные эмпирические частости с накопленными теоретическими частостями. Для 1-го разряда теоретическая частость определяется по формуле:

f*теор=1/k

9Все формулы приведены для дискретных признаков, которые могут быть выражены целыми числами, например: порядковый номер, количество испытуемых, количественный состав группы и т.п.

где k - количество разрядов (в данном случае - позиций цвета).

Для рассматриваемого примера:

f*теор =1/8=0,125

Эта теоретическая частость относится ко всем 8-и разрядам. Действительно, вероятность попадания желтого (или любого другого) цвета на каждую из 8-и позиций при случайном выборе составляет 1/8, т.е. 0,125.

Накопленные теоретические частости для каждого разряда определяем суммированием.

Для 1-го разряда накопленная теоретическая частость равна теоретической частости попадания в разряд:

f*т1=0,125

Для 2-го разряда накопленная теоретическая частость представляет собой сумму теоретических частостей 1-го и 2-го разрядов:

f*т1+2=0,125+0,125=0,250

Для 3-го разряда накопленная теоретическая частость представляет собой сумму накопленной к предыдущему разряду теоретической частости с теоретической частостью данного разряда:

f*т1+2+3=0,250+0,125=0,375

Можно определить теоретические накопленные частости и путем умножения:

S f*тj= f*теор*j

где f*теор  - теоретическая частость;

j - порядковый номер разряда.

Занесем рассчитанные накопленные теоретические частости в четвертый столбец таблицы (Табл. 4.17).

Теперь нам осталось вычислить разности между эмпирическими и теоретическими накопленными частостями (столбцы 3-й и 4-й). В пятый столбец записываются абсолютные величины этих разностей, обозначаемые как d.

Определим по столбцу 5, какая из абсолютных величин разности является наибольшей. Она будет называться dmax. В данном случае dmax =0,135.

Теперь нам нужно обратиться к Табл. X Приложения 1 для определения критических значений dmax при n=102.

Таблица 4.17

Расчет критерия при сопоставлении распределения выборов желтого цвета с равномерным распределением (n=102)

Позиция желтого цвета	Эмпирическая частота	Эмпирическая частость	Накопленная эмпирическая частость	Накопленная теоретическая частость	Разность
1	24	0,235	0,235	0,125	0,110
2	15	0,147	0,382	0,250	0,132
3	13	0,128	0,510	0,375	0,135
4	8	0,078	0,588	0,500	0,088
5	15	0,147	0,735	0,625	0,110
6	10	0,098	0,833	0,750	0,083
7	9	0,088	0,921	0,875	0,046
8	8	0,079	1,000	1,000	0,000
Суммы	102	1,000

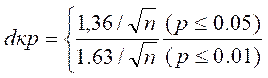
Для данного случая, следовательно,

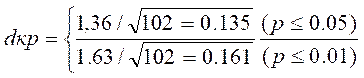
Очевидно, что чем больше различаются распределения, тем больше и различия в накопленных частостях. Поэтому нам не составит труда распределить зоны значимости и незначимое™ по соответствующей оси:

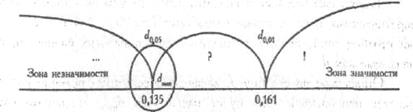
dэмп =0,135

dэмп- dкр

 

Ответ: Но отвергается при р=0,05. Распределение желтого цвета по восьми позициям отличается от равномерного распределения. Представим все выполненные действия в виде алгоритма

АЛГОРИТМ 14

Расчет абсолютной величины разности d между эмпирическим и равномерным распределениями

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2.  Подсчитать относительные эмпирические частоты (частости) для каждого разряда по формуле:

ƒ*эмп = ƒэмп /n

где ƒэмп  - эмпирическая частота по данному разряду;

п - общее количество наблюдений.

Занести результаты во второй столбец.

3.         Подсчитать накопленные эмпирические частости ∑f*j по формуле:

∑f*j=∑f*j -1+f*j

где ∑f*j -1 - частость, накопленная на предыдущих разрядах;

j - порядковый номер разряда;

f*j:- эмпирическая частость данного j-ro разряда.

Занести результаты в третий столбец таблицы.

4.         Подсчитать накопленные теоретические частости для каждого разряда по формуле:

∑f*тj=∑f*тj -1+f*тj

где =∑f*тj -1 - теоретическая частость, накопленная на предыдущих разрядах;

j - порядковый номер разряда;

ƒ*тj : - теоретическая частость данного разряда. Занести результаты в третий столбец таблицы.

5.Вычислить разности между эмпирическими и теоретическими накопленными частостями по каждому разряду (между значениями 3-го и 4-го столбцов).

6.Записать в пятый столбец абсолютные величины полученных разностей, без их знака. Обозначить их как d.

7.Определить по пятому столбцу наибольшую абсолютную величину разности - dmax.

8.По Табл. X Приложения 1 определить или рассчитать критические значения dmax для данного количества наблюдений n.

Если dmax равно критическому значению d или превышает его, различия между распределениями достоверны.

Пример 2: сопоставление двух эмпирических распределений

Интересно сопоставить данные, полученные в предыдущем примере, с данными обследования X. Кларом 800 испытуемых (Klar H., 1974, р. 67). X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отличается от равномерного. Для сопоставлений им использовался метод χ2. Полученные им эмпирические частоты представлены в Табл. 4.18.

Таблица 4.18

Эмпирические частоты попадания желтого цвета на каждую из 8 позиций в исследовании X. Клара (по: Klar H., 1974) (п=800)

Разряды-позиции желтого цвета	1	2	3	4	5	6	7	8	Сумма
Эмпирические частоты	98	113	116	87	91	112	97	86	800

Сформулируем гипотезы.

Н0: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара не различаются.

H1: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара отличаются друг от друга.

Поскольку в данном случае мы будем сопоставлять накопленные эмпирические частости по каждому разряду, теоретические частости нас не интересуют.

Все расчеты будем проводить в таблице по алгоритму 15.

АЛГОРИТМ 15

Расчет критерия λ при сопоставления двух эмпирических распределений

1.Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и в распределении 2 (второй столбец).

2.Подсчитать эмпирические частости по каждому разряду для распределения 1 по формуле:

ƒ*э=ƒэ/n1

где ƒэ  - эмпирическая частота в данном разряде;

n1[ - количество наблюдений в выборке.

Занести эмпирические частости распределения 1 в третей столбец.

3.         Подсчитать эмпирические частости по каждому разряду для распределения 2 по формуле:

ƒ*э=ƒэ/n2

где ƒэ  - эмпирическая частота в данном разряде;

n2 - количество наблюдений во 2-й выборке.

Занести эмпирические частости распределения 2 в четвертый столбец таблицы.

4.         Подсчитать накопленные эмпирические частости для распределения 1 по формуле:

∑ƒ*j =∑ƒ*j-1 +ƒ*j

где ∑ƒ*j-1 - частость, накопленная на предыдущих разрядах;

j - порядковый номер разряда;

ƒ*j-1 - частости данного разряда.

Полученные результаты записать в пятый столбец.

5.Подсчитать накопленные эмпирические частости для распределения 2 по той же формуле к записать результат в шестой столбец.

6.Подсчитать разности между накопленными частостями по каждому разряду.
Записать в седьмой столбец абсолютные величины разностей, без их знака.
Обозначить их как d.

7.Определить по седьмому столбцу наибольшую абсолютную величину разности

4пах-

8.         Подсчитать значение критерия λ по формуле:

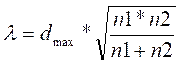
где  n1 - количество наблюдений в первой выборке;

n2 - количество наблюдении во второй выборке.

9.         По Табл. XI Приложения 1 определить, какому уровню статистической значимости соответствует полученное значение λ.

Если λэмп > 1,36, различия между распределениями достоверны.

Последовательность выборок может быть выбрана произвольно, так как расхождения между ними оцениваются по абсолютной величине разностей. В нашем случае первой будем считать отечественную выборку, второй - выборку Клара.

 

Таблица 4.19

Расчет критерия при сопоставлении эмпирических распределений

желтого цвета в отечественной выборке (n1=102)

и выборке Клара (п2=:800)

Позиция желтого цвета	Эмпирические частоты		Эмпирические частости		Накоплены эмпирические частности		Разность ∑ƒ*1-∑ƒ*2
	ƒ1	ƒ2	ƒ*1	ƒ*2	∑ƒ*1	∑ƒ*2
1	24	98	0,235	0,123	0,235	0,123	0,112
2	15	113	0,147	0,141	0,382	0,264	0,118
3	13	116	0,128	0,145	0,510	0,409	0,101
4	8	87	0,078	0,109	0,588	0,518	0,070
5	15	91	0,147	0,114	0,735	0,632	0,103
6	10	112	0,098	0,140	0,833	0,772	0,061
7	9	97	0,088	0,121	0,921	0,893	0,028
8	8	86	0,079	0,107	1,000	1,000	0
Суммы	102	800	1,000	1,000

Максимальная  разность  между  накопленными   эмпирическими частостями составляет 0,118 и падает на второй разряд.

В соответствии с пунктом 8 алгоритма 15 подсчитаем значение λ:

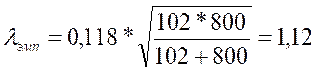
По Табл. XI Приложения 1 определяем уровень статистической
значимости полученного значения: р=0,16                         :

Построим для наглядности ось значимости.

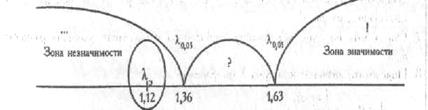
На оси указаны критические значения λ соответствующие принятым уровням значимости: λ0,05=1,36, λ0,01=1,63.

Зона значимости простирается вправо, от 1,63 и далее, а зона незначимости – влево, от 1,36 к меньшим значениям.

λ эмп < λкр

Ответ: Но принимается. Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара совпадают. Таким образом, распределения желтого цвета в двух выборках не различаются, но в то же время они по-разному соотносятся с равномерным распределением: у Клара отличий от равномерного распределения не обнаружено, а 8 отечественной выборке различия обнаружены (р<0,05). Возможно, картину могло бы прояснить применение другого метода?

Е.В. Гублер (1978) предложил сочетать использование критерия λ с критерием φ* (угловое преобразование Фишера).

Об этих возможностях сочетания методов λ и φ* мы поговорим в следующей лекции.

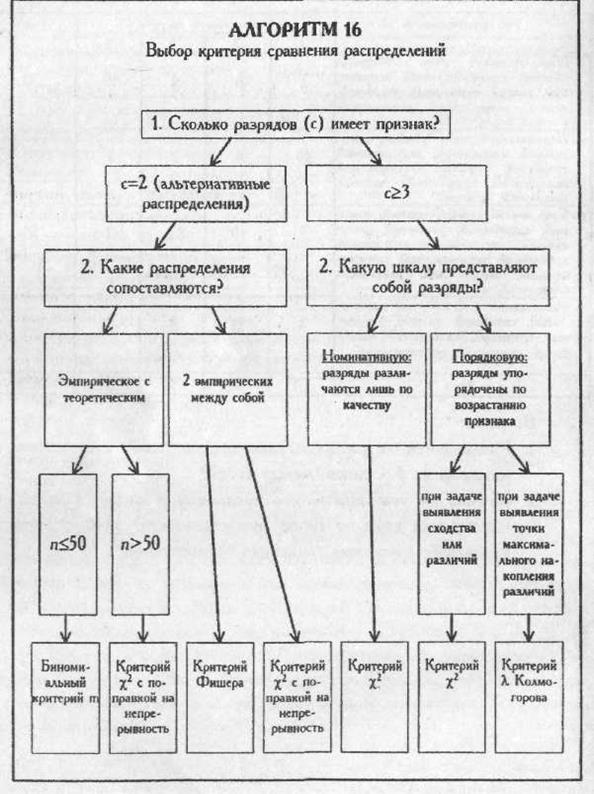
Алгоритм выбора критерия для сравнения распределений