Многофункциональные критерии как эффективные заменители традиционных критериев

Как было показано в предыдущих параграфах, многофункциональные критерии, главным образом критерий φ*, применим к решению всех трех типов задач, рассмотренных в Темах 3-5: сопоставление уровней, определение сдвигов и сравнение распределений признака. В тех случаях, когда обследованы две выборки испытуемых, критерий φ* может эффективно заменять или, по крайней мере, эффективно дополнять традиционные критерии: Q - критерий Розенбаума, U - критерий Манна-Уитни, критерий χ2 Пирсона и критерий λ Колмогорова-Смирнова.

В особенности полезна такая замена в следующих случаях:

Случай 1. Другие критерия неприменимы

Часто бывает так, что критерий Q неприменим вследствие совпадения диапазонов двух выборок, а критерий U неприменим вследствие того, что количество наблюдений п>60.

В качестве примера сошлемся на задачу сравнения сдвигов оценок в экспериментальной и контрольной группах после просмотра видеозаписи и чтения текста о пользе телесных наказании (см. параграф 2 Темы 4).

Сдвиги в двух группах являются показателями, полученными независимо в двух группах испытуемых. Задача сравнения таких показателей сдвига - это частный случай задачи сопоставления двух групп по уровню значений какого-либо признака. Такие задачи решаются с помощью критериев Q Розенбаума и U Манна-Уитни (см. Табл. 3.1). Сводные данные по сдвигам в двух группах представлены в Табл. 5.14.

Таблица 5.14

Эмпирические частоты сдвигов разной интенсивности и направления в экспериментальной и контрольной группах после предъявления видеозаписи или письменного текста

В экспериментальной группе значения сдвигов варьируют от —2 до +2, а в контрольной группе от —2 до +5. Критерий Q неприменим. Критерий U неприменим, поскольку количество наблюдений (сдвигов) в каждой группе больше 60.

Применяем критерий φ*. Построим вначале четырехклеточную таблицу для положительных сдвигов, а затем - для нулевых.

Таблица 5.15

Четырехклеточная таблица для подсчета критерия φ* при сопоставлении долей положительных сдвигов в экспериментальной и контрольной

группах

Сформулируем гипотезы.

H0: Доля положительных сдвигов в экспериментальной группе не больше, чем в контрольной.

       Н1: Доля положительных сдвигов в экспериментальной группе больше, чем в контрольной.

Далее действуем по Алгоритму 17.

φ1(34,4%)=1.254

φ2(18,5%)=0,889

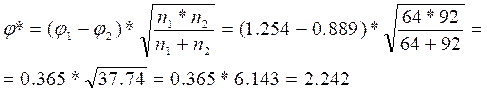
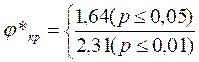
Мы можем и точно определить уровень статистической значимости полученного результата по Табл. ХШ Приложения 1:

при φ* эмп=2,242     р=0,013.

Ответ: H0 отклоняется. Принимается Н1.  Доля положительных сдвигов  в  экспериментальной группе больше,  чем в контрольной (p<0.013)

Теперь перейдем к вопросу о меньшей доле нулевых сдвигов в экспериментальной группе.

Таблица 5.16

Четырехклеточная таблица для подсчета критерия φ* при сопоставлении долей нулевых сдвигов в экспериментальной и контрольной группах

Сформулируем гипотезы.

Но: Доля нулевых сдвигов в контрольной группе не больше, чем в экспериментальной.

H1: Доля нулевых сдвигов в контрольной группе больше, чем в экспериментальной.

Далее действуем по Алгоритму 17.

φ1(70,7%)=1.998

φ2(59,4%)=1.760

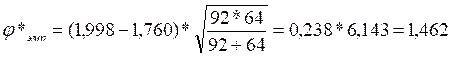
φ*эмп < φ*кр

Ответ: H0 принимается. Доля нулевых сдвигов в контрольной группе не больше, чем в экспериментальной.

Итак, доля положительных сдвигов в экспериментальной группе больше, но доля нулевых сдвигов - примерно такая же, как и в контрольной группе. Отметим, что в критерии знаков G все нулевые сдвиги были исключены из рассмотрения, поэтому полученный результат дает дополнительную информацию, которую не мог дать критерий знаков.

Случай 2. Другие критерии неэффективны или слишком громоздки

В качестве примера можно указать на задачу с сопоставлением показателей недостаточности в группах с большей и меньшей энергией вытеснения (см. Табл. 5,4).

Критерий Q дает незначимый результат:

Q =S1 +S2=4+0=4

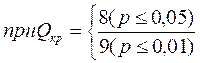
Критерий U в данном случае применим и даже дает значимый результат (Uэмп=l54,5; р≤0,05), однако ранжирование показателей, многие из которых имеют одно и то же значение (например, значение 30 баллов встречается 13 раз), представляет определенные трудности.

Как мы помним, с помощью критерия φ* удалось доказать, что наиболее высокие показатели недостаточности (30 и более баллов) встречаются в группе с большей энергией вытеснения чаще, чем в группе с меньшей энергией вытеснения (р=0,008) и что, с другой стороны, самые низкие (нулевые) показатели встречаются чаще также в этой группе (р≤0,05).

Другим примером может служить задача сопоставления распределения выборов желтого цвета в отечественной выборке и в выборке Х.Клара (см. параграф 4.3).

Критерий λ не выявил достоверных различий между двумя распределениями, однако позволил нам установить точку максимального накопленного расхождения между ними. Из Табл. 4.19 следует, что такой точкой является вторая позиция желтого цвета. Построим четырехклеточную таблицу, где "эффектом" будет считаться попадание желтого цвета на одну из первых двух позиций.

Таблица 5.17

Четырехклеточная таблица для расчета φ* при сопоставлении отечественной выборки (n1=102) и выборки Х.Клара (n2=800) по положению желтого цвета в ряду предпочтений

Сформулируем гипотезы.

Но: Доля лиц, помещающих желтый цвет на одну из первых двух позиций, в отечественной выборке не больше, чем в выборке Х.Клара.

H1: Доля лиц, поместивших желтый цвет на одну из первых двух позиции, в отечественной выборке больше, чем в выборке X. Клара.

Далее действуем по Алгоритму 17.

φ1(38,2%)=1.333

φ2(26,4%)=1,079

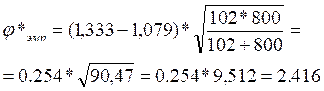
Как мы помним,

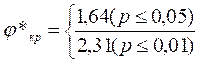
φ*эмп > φ*кр

Ответ: H0 отклоняется. Принимается Н1: Доля лиц, поместивших желтый цвет на одну из первых двух позиций, в отечественной выборке больше, чем в выборке X.Клара (р≤0,01).

Мы еще раз столкнулись с тем случаем, когда критерий X сам по себе не выявляет достоверных различий, но помогает максимально использовать возможности критерия φ*.

Случай 3. Другие критерии слишком трудоемки

Этот случай чаще всего относится к критерию χ2. Заменить его критерием φ* можно при условии, если сравниваются распределения признака в двух выборках, а сам признак принимает всего два значения5.

5.В принципе признак может принимать и большее количество значении, так как любую шкалу, как мы убедились, можно свести к альтернативной шкале "Есть эффект" - "Нет эффекта".

В качестве примера можно привести задачу с соотношением мужских и женских имен в записных книжках двух психологов (см. п. 4.2, Табл. 4.11).

Преобразуем Табл. 4.11 в четырехклеточную таблицу, где "эффектом* будем считать мужские имена.

Таблица 5.18

Четырехклеточная таблица для подсчета φ* при сопоставлении записных книжек двух психологов по соотношению мужских и женских имен

Сформулируем гипотезы.

Н0: Доля мужских имен в записной книжке С. не больше, чем в записной книжке X.

H1: Доля мужских имен в записной книжке С. больше, чем в записной книжке X.

Далее действуем по алгоритму.

φ1(35,1%)=1.268

φ2(32,8%)=1,220

По Табл. XIII Приложения 1 определяем, какому уровню достоверности соответствует это значение. Мы видим, что такого значения вообще нет в таблице.

Построим "ось значимости".

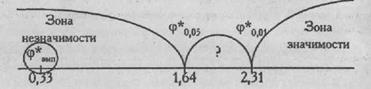
Полученное эмпирическое значение - далеко в "зоне незначимости».

φ*эмп > φ*кр

Ответ: Но принимается. Доля мужских имен в записной книжке психолога С. не больше, чем в записной книжке психолога X.

Исследователь сам может решить для себя, какой метод ему в данном случае удобнее применить – χ2 или φ*. Похоже, что во втором случае меньше расчетов, хотя чуда не произошло: различия по-прежнему недостоверны.

Итак, мы убедились, что критерий φ* Фишера может эффективно заменять традиционные критерии в тех случаях, когда их применение невозможно, неэффективно или неудобно по каким-то причинам.

Биномиальный критерий m может служить заменой критерия χ2 в случае альтернативных распределений или в случае, когда признак может принимать одно из нескольких значений и вероятность того, что он примет определенное значение, известна.