Подготовка данных к дисперсионному анализу

1) Создание комплексов

Лучше всего для каждого испытуемого создать отдельную карточку, куда были бы занесены данные по всем исследованным признакам. Дело в том, что в процессе анализа у исследователя могут измениться гипотезы. Потребуется создавать, быть может, не один, а множество дисперсионных комплексов, различающихся как по факторам, так и по результативным признакам. Карточки помогут нам быстро создавать новые дисперсионные комплексы. Благодаря карточкам мы сразу увидим, равномерно ли распределяются данные по градациям в случае, если за фактор мы решили принять один из исследованных психологических признаков. С помощью карточек мы можем помочь себе выделить три, четыре или более градаций этого фактора, например, уровни мотивации, настойчивости, креативности и др.

2)  Уравновешивание комплексов

Комплекс, в котором каждая ячейка представлена одинаковым количеством наблюдений, называется равномерным. Равномерность комплекса позволяет нам обойти требование равенства дисперсий в каждой из ячеек комплекса (Шеффе Г., 1980).

Равномерные комплексы позволяют также избежать значительных трудностей, которые неизбежно возникают при обсчете неравномерных, или неортогональных, комплексов. В настоящем методическом пособии приведены алгоритмы расчета лишь для равномерных комплексов. С методами обсчета неравномерных комплексов можно ознакомиться у Н.А. Плохинского (1970), Г.В.

В случае, если в разных градациях комплекса оказалось неравное количество наблюдений, необходимо отсеять некоторые из них. Если в комплексе со связанными выборками кто-либо из испытуемых не был подвергнут одному из условий действия переменной (градаций фактора), то его данные исключаются. Если же комплекс включает независимые выборки, каждая из которых была подвергнута определенному условию воздействия (градации фактора), то "лишние" испытуемые в какой-либо из ячеек комплекса отсеиваются путем случайного выбора необходимого количества карточек.

3)  Проверка нормальности распределения результативного признака.

Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда известно или доказано, что распределение признака является нормальным (Суходольский Г.В., 1972; Шеффе Г., 1980 и др.). Строго говоря, перед тем, как применять дисперсионный анализ, мы должны убедиться в нормальности распределения результативного признака. Нормальность распределения результативного признака можно проверить путем расчета показателей асимметрии и эксцесса и сопоставления их с критическими значениями (Пустыльник Е,И., 1968* Плохинский Н.А., 1970 и др.).

Произведем необходимые расчеты на примере вопроса 3 Темы №9, в котором анализируется длительность мышечного волевого усилия.

Действовать будем по следующему алгоритму:

а)   определим показатели асимметрии и эксцесса по формулам Н.А.Плохинского и сопоставим их с критическими значениями, указанными Н.А. Плохинским;

б) рассчитаем критические значения показателей асимметрии и эксцесса по формулам Е.И. Пустыльника и сопоставим с ними эмпирические значения;

в) если эмпирические значения показателей окажутся ниже критических, сделаем вывод о том, что распределение признака не отличается от нормального.

Таблица 7.1

Вычисление показателей асимметрии и эксцесса по показателю длительности попыток решения анаграмм

Для расчетов в Табл. 7.1 необходимо сначала определить среднюю арифметическую по формуле:

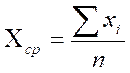
где xi ; - каждое наблюдаемое значение признака;

   п - количество наблюдений.

В данном случае:

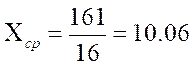
Стандартное отклонение (сигма) вычисляется по формуле:

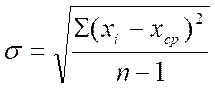
где   xi - каждое наблюдаемое значение признака;

         xср - среднее значение (среднее арифметическое);

         n - количество наблюдений.

В данном случае:

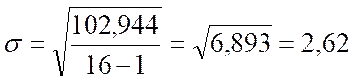
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:

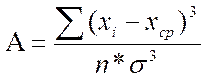
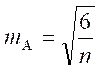
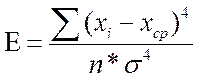
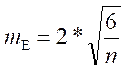
где (xi – xср) – центральные отклонения;

σ – стандартное отклонение

n –количество испытуемых

В данном случае:

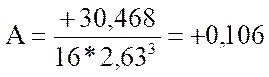
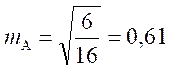
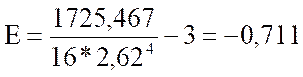
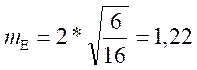
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:

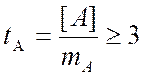
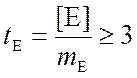
В данном случае:

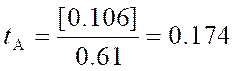
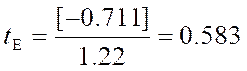
Мы видим, что оба показателя не превышают в три раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального.

Теперь произведем проверку по формулам Е.И. Пустыльника. Рассчитаем критические значения для показателей А и Е:

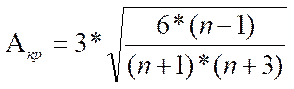
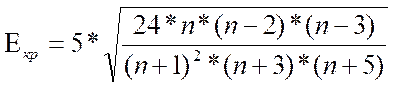
где n – количество наблюдений.

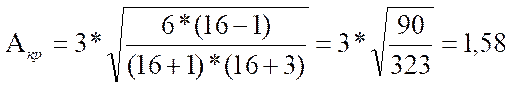
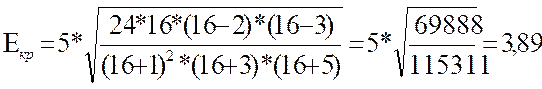
Аэмп =0,106

Аэмп < Акр

Еэмп = -0,711

Еэмп < Екр

Итак, оба варианта проверки, по Н.А. Плохинскому и по Е.И. Пустыльнику, дают один и тот же результат: распределение результативного признака в данном примере не отличается от нормального распределения.

Можно выбрать любой из двух предложенных вариантов проверки и придерживаться его. При больших объемах выборки, по-видимому, стоит производить расчет первичных статистик (оценок параметров) на ЭВМ.

4) Преобразование эмпирических данных с целью упрощения расчетов

НА. Плохинский указывает на возможность следующих преобразований:

1) все наблюдаемые значения можно разделить на одно и то же число k,

   например перевести показатели из миллиметров в сантиметры и т.п.;

2) все наблюдаемые значения можно умножить на одно и то же число k,
например для того, чтобы избавиться от дробных значений;

3) от всех наблюдаемых значений можно отнять одно и то же число А,
например наименьшее значение;

4) можно сделать двойное преобразование: из каждого значения вычесть число А, а полученный результат разделить на другое число k.

При всех этих преобразованиях результативного признака показатели соотношения дисперсий получаются точными и не требуют никаких поправок.

Средние величины изменяются, но их можно восстановить, умножая среднюю величину на число k или деля ее на k (варианты 1 и 2) или прибавляя к средней число А (вариант 3) и т. п. Стандартное отклонение изменяется только при введении множителя или делителя; полученный результат затем придется либо разделить на число k, либо умножить на него (Плохинский Н.А.,1964, с.34-36; Плохинский Н.А., 1970, с.71-72).

В последующих трех параграфах будет рассмотрен метод однофакторного анализа в двух вариантах:

а) для дисперсионных комплексов, представляющих данные одной и той же выборки испытуемых, подвергнутой влиянию разных условий (разных градаций фактора);

б) для дисперсионных комплексов, в которых влиянию разных условий (градаций фактора) были подвергнуты разные выборки испытуемых.

Первый вариант называется однофакторным дисперсионным анализом для связанных выборок, второй - для несвязанных выборок.

Все предложенные алгоритмы расчетов предназначены для равномерных комплексов, где в каждой ячейке представлено одинаковое число наблюдений.