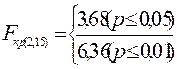Дисперсионный анализ для связанных выборок

Назначение метода

Метод дисперсионного анализа для связанных выборок применяется в тех случаях, когда исследуется влияние разных градаций фактора или разных условий на одну и ту же выборку испытуемых.

Градаций фактора должно быть не менее трех.

Непараметрический вариант этого вида анализа - критерий Фридмана χ2r.

Описание метода

В данном случае различия между испытуемыми - возможный самостоятельный источник различий. В схеме однофакторного анализа для несвязанных выборок различия между условиями в то же время отражали различия между испытуемыми. Теперь различия между условиями могут проявиться только вопреки различиям между испытуемыми.

Фактор индивидуальных различий может оказаться более значимым, чем фактор изменения экспериментальных условий. Поэтому нам необходимо учитывать еще одну величину - сумму квадратов сумм индивидуальных значений испытуемых.

Графическое представление метода

На Рис. 7.3 представлена кривая изменения времени решения анаграмм разной длины: четырехбуквенной, пятибуквенной и шестибуквенной. Однофакторный дисперсионный анализ для связанных выборок позволит определить, что перевешивает - тенденция, выраженная этой кривой, или индивидуальные различия, диапазон которых представлен на графике в виде вертикальных линий — от минимального до максимального значения.

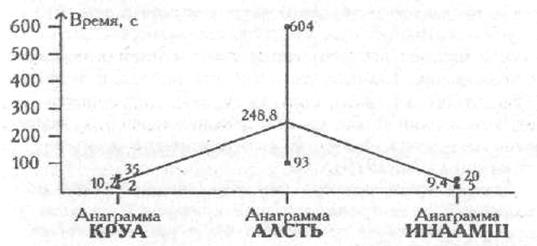
Рис. 7.3. Изменение времени работы над разными анаграммами у тати испытуемых; вертикальными линиями отображены диапазоны изменчивости признака е разных условиях от минимального значения (снизу) до максимального значения (сверху)

Ограничения метода дисперсионного анализа для связанных выборок

1.  Дисперсионный анализ для связанных выборок требует не менее трех градаций фактора и не менее двух испытуемых, подвергшихся воздействию каждой из градаций фактора.

2.  Должно соблюдаться правило равенства дисперсий в каждой ячейке комплекса. Это условие косвенно выполняется за счет одинакового количества наблюдений в каждой ячейке комплекса. Предлагаемая схема расчета ориентирована только на такие равномерные комплексы.

3.  Результативный признак должен быть нормально распределен в исследуемой выборке.

В приводимом ниже примере показатели асимметрии и эксцесса составляют:

А=218

тА=0,632;

tA =2,18/0,632=3,45;

E=4,17;

ME =l,264;

tE =4,17/1,264=3,30.

Таким образом, распределение показателей 5-тй- человек, составляющих дисперсионный комплекс, несколько отличается от нормального: tA>3; tE>3. Однако в целом по выборке распределение нормальное:

n=22;

A=1,26;

тА=0,522

 tA=2,41<3;

E=2,29;

mE=1,044;

tE=2,19<3.

По-видимому, необходимо удовлетвориться тем, что в выборке в целом результативный признак распределен нормально. Случайно отобранные 5 человек распределением своих оценок демонстрируют некоторое отклонение. Однако, если бы мы выбирали испытуемых таким образом, чтобы распределение их оценок подчинялось нормальному закону, это нарушило бы правило рандомизации - случайности отбора объектов без учета значений результативного признака при отборе (Плохинский Н.А. 1970).

Данные этого примера нам уже знакомы. Они использовались для иллюстрации непараметрического критерия Фридмана χ2r. Использование здесь этого же примера позволит нам сопоставить результаты, получаемые с помощью непараметрических и параметрических методов.

Пример

Группа из 5 испытуемых была обследована с помощью трех экспериментальных заданий, направленных на изучение интеллектуальной настойчивости (Сидоренко Е. В., 1984). Каждому испытуемому индивидуально предъявлялись последовательно три одинаковые анаграммы: четырехбуквенная, пятибуквенная и шестибуквенная. Можно ли считать, что фактор длины анаграммы влияет на длительность попыток ее решения?

Сформулируем гипотезы.

Наборов гипотез в данном случае два.

Набор А.

Но(А): Различия в длительности попыток решения анаграмм разной длины являются не более выраженными, чем различия, обусловленные случайными причинами.

Н1(А): Различия в длительности попыток решения анаграмм разной длины являются более выраженными, чем различия, обусловленные случайными причинами. Набор Б.

Но(Б): Индивидуальные различия между испытуемыми являются не более выраженными, чем различия, обусловленные случайными причинами.

Н1(Б):  Индивидуальные различия между испытуемыми являются более выраженными, чем различия, обусловленные случайными причинами.

Таблица 7.5

Длительность попыток решения анаграмм (сек)

Установим все промежуточные величины, необходимые для расчета критерия F.

Таблица 7.6

Расчет промежуточных величин для критерия F в примере об анаграммах

Мы по-прежнему помним разницу между квадратом суммы и суммой квадратов!

Последовательность расчетов приведена в Табл. 7.7.

Таблица 7.7.

Последовательность операций в однофакторной модели дисперсионного анализа для связанных выборок

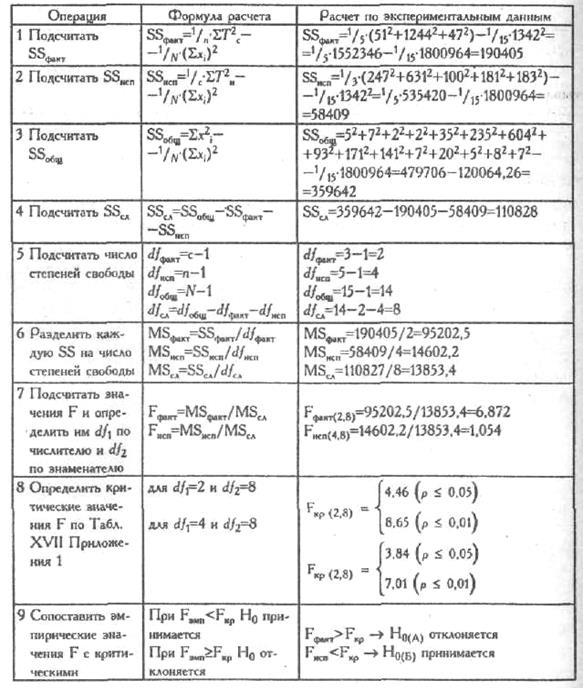Последовательность операций в однофакторной модели

Примечание: (См.Приложение 2).

Вывод:

Но(А) отклоняется. Различия в объеме воспроизведения слов в разных условиях являются более выраженными, чем различия, обусловленные случайными причинами (р<0,05).

Но(Б) принимается: Индивидуальные различия между испытуемыми являются не более выраженными, чем различия, обусловленные случайными причинами.

            Однако, судя по Рис. 7.3, мы не можем утверждать, что срабатывает фактор длины анаграммы. Более значимыми оказываются качественные, а не количественные различия между анаграммами. Как мы уже имели возможность убедиться (см. параграфы 3.4 и 3.5), непараметрический L - критерий Пейджа подтверждает тенденцию увеличения индивидуальных показателей при переходе от анаграммы КРУА к анаграмме ИНААМШ, а затем к анаграмме АЛСТЬ (р<0,01). Значимые различия были получены и с помощью критерия Фридмана χ2r

(р=0,0085).

Итак, непараметрические критерии позволяют нам констатировать более высокий уровень значимости различий между условиями!

Зачем же тогда использовать достаточно сложный дисперсионный анализ? Для того, чтобы подобрать существенные факторы, которые могут стать основой для формирования двух-, трех- и более факторных дисперсионных комплексов, позволяющих оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие.

Приложение 1

Таблица 7.4.

Последовательность операций в однофакторном дисперсионном анализе для несвязанных выборок

Приложение 2

Таблица 7.7.

Последовательность операций в однофакторном дисперсионном анализе для связанных выборок