(ЗЛП на минимизацию)
Предположим, что в дневной рацион животных должны входить питательные вещества двух видов в количестве, заданном в таблице.
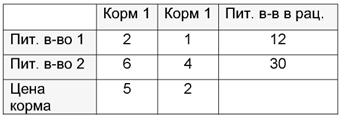
Имеется возможность составлять рацион из кормов двух видов, для которых задано содержание питательных веществ в единице корма и цена одной единицы каждого из видов кормов. При удовлетворении условий по необходимому содержанию питательных веществ в данном рационе требуется достичь его минимальной стоимости.
Пусть х1 и х2 - содержание в данном рационе единиц корма 1-го и 2-го вида соответственно. Общую стоимость дневного рациона запишем, используя цены на корма:
![]()
Ограничения имеют следующую структуру:
содержание пит, веществ в рационе ≥ min кол-во пит, в-в.
Используя для записи левой части введенные неизвестные, получим
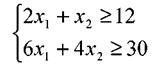
Добавив к полученным ограничениям условия неотрицательности (х1 равно нулю, если корм i не используется в рационе), окончательно запишем ЗЛП.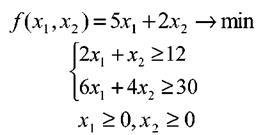
В приведенных примерах все ограничения имеют вид линейных неравенств. Это, так называемые, нежесткие ограничения (ресурс может быть израсходован полностью, а может и частично). Однако можно ставить и жесткие ограничения в виде линейных уравнений. Так, в первом примере, требование полного использования ресурса 1-го вида
приводит к ограничению:![]()
Теория графов и графовые сети (или просто графы) используются практически во всех областях знаний, в том числе, в компьютерной науке и практике. Основное достоинство графов в том, что их можно рисовать на бумаге или экранах компьютеров в виде точек соединенных стрелками и/или линиями. Вместе с тем, связанный граф представляется формально с помощью наборов бинарных отношений и/или множеств, каждое их которых состоит из двух элементов. Графы рисуют на бумаге не только те кто понимают теорию графов, но и люди, которые никогда о ней не слышали. К примеру, любой администратор, изображающий структуру, подчиненных ему подразделений в виде прямоугольников и стрелок между ними, по сути дела, рисует связанный ориентированный граф, хотя он и не знает об этом.
Графом называется набор точек (эти точки называются вершинами), некоторые из которых объявляются смежными (или соседними). Считается, что смежные вершины соединены между собой ребрами (или дугами).
Таким образом, ребро определяется парой вершин. Два ребра, у которых есть общая вершина, также называются смежными (или соседними).
Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой).
Помимо этого, в теории графов рассматриваются также мультиграфы – это такие графы, в которых могут быть петли (т. е. некоторая вершина соединена сама с собой ребром) или некоторые пары вершины могут быть соединены между собой несколькими ребрами.
Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.
Путь в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).
Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.
Последовательности вершин (рис. 1): 1–2–3–4–2–5 не простой путь, а маршрут; последовательности 1–2–3–4–7–5 и 1–2–5 – простые пути; 1–2–3–4–2–5–6–1 –это цикл (но не контур); 1–2–5–6–1 – это контур.
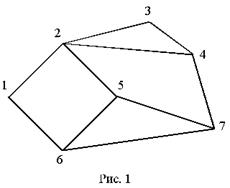
Если имеется некоторый маршрут из вершины t в вершину s, заданный в виде последовательности ребер, которые в этом случае приобрели направление, и если в этот маршрут входит ребро, соединяющее вершины (i, j), то это ребро по отношению к вершине i называют иногда прямой дугой, а по отношению к вершине j – обратной дугой (или обратным ребром).
Граф называется связным, если любые две его вершины можно соединить маршрутом (или путем). На рис. 1 изображен связный граф.
Ребро, при удалении которого граф перестает быть связным, иногда называют мостом или перешейком.
Следующее определение имеет смысл только для графов или мультиграфов без петель (но не для орграфов).
Степень вершины – это число ребер, входящих в эту вершину. Вершина называется висячей, если ее степень равна единице.
Лемма 1. Если степень всех вершин в графе больше или равна двум, то граф обязательно содержит контур.
Поможем написать любую работу на аналогичную тему

