При моделировании экономических задач, таких как задачи управления и планирования производства, определения оптимального размещения оборудования, оптимального плана производства, оптимального плана перевозок грузов (транспортная задача), распределения кадров и др., может быть положена гипотеза линейного представления реального мира.
Математические модели таких задач представляются линейными уравнениями. Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.
Линейные математические модели также используются в нелинейных системах при условии, если эта нелинейная система условно линеаризирована.
В общем виде система линейных уравнений имеет вид:
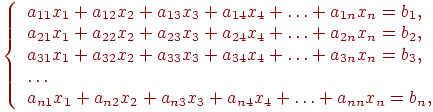
Где aij- коэффициенты при неизвестных системы, bi- свободные члены, xj- неизвестные системы, 
- номер строки, 
- номер столбца, n - порядок системы.
В матричной форме система линейных уравнений имеет вид:
где
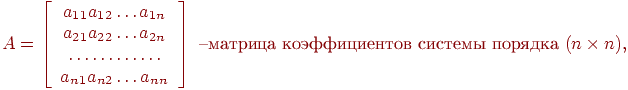
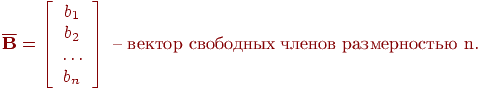
Численные методы решения систем линейных уравнений (СЛУ) можно разделить на две группы:
1. точные или прямые методы,
2. приближенные методы.
Приближенные методы реализуют на ЭВМ нахождение корней с заданной точностью и являются итерационными методами.
Точные методы позволяют получить решение системы за конечное число итераций. К точным методам относятся:
- правило Крамера,
- метод Гаусса,
- метод прогонки.
Задачей линейного программирования (ЗЛП) называется задача отыскания экстремума (максимума или минимума) линейной функции от нескольких переменных при линейных ограничениях на эти переменные.
Пример: Найти максимальное значение функции
при следующих ограничениях на переменные x1 и x2
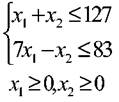
Приведенная задача есть ЗЛП максимизации от двух переменных с ограничениями-неравенствами (могут быть и ограничения-равенства). Линейная функция f называется функцией цели, или целевой функцией.
Ограничения x1 ≥0, x2 ≥0 называются ограничениями неотрицательности (или условиями неотрицательности), а система линейных неравенств и (или) уравнений называется системой ограничений ЗЛП. Запись ЗЛП с ограничениями-неравенствами выглядит следующим образом
- Это целевая функция
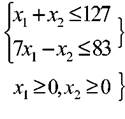
ЗЛП является удобной математической моделью для большого числа экономических задач (планирование производства, расходование ресурсов, раскрой материалов, транспортные перевозки и т.д.). Рассмотрим на примерах процесс построения математической модели (в виде ЗЛП на максимум или минимум) для ряда экономических задач.
Поможем написать любую работу на аналогичную тему