Задача планирования производства продукции (ЗЛП на максимизацию).

Основа построения экономических моделей в виде ЗЛП - это, прежде всего, правильный выбор параметров экономической задачи (или некоторого процесса), через которые требуемая цель выражалась бы в виде линейной целевой функции, а ограничения на процесс записывались бы в виде системы линейных уравнений или неравенств.

Некоторое предприятие в течение планового периода выпускает 2 вида продукции, например, табуретки и стулья. При их производстве используются три вида ресурсов. Данные по их расходу на выпуск одного изделия, запасы ресурсов, а также прибыль от реализации единицы продукции приведены в таблице. Требуется спланировать количество выпускаемых табуреток и стульев таким образом, чтобы при данных условиях производства полученная прибыль была максимальна. Итак, цель задачи - получение максимальной прибыли. Выберем в качестве параметров, характеризующих процесс планирования производства

продукции, число выпускаемых табуреток (переменная x1) и

выпускаемых  стульев (переменная  x1). Выразим через выбранные неизвестные суммарную прибыль от реализации всей продукции f(x1, x2)=4 x1+5 x2

Она включает в себя прибыль от реализации всех табуреток (4х1) и выпускаемых стульев  (5х2). Цель задачи (максимизация прибыли) запишется в виде

f(x1, x2) = 4х1 +5х2 max

Перейдем    к    формулировке    ограничений.    Структура    всех    трех ограничений одинакова

РАСХОД   РЕСУРСА      ≤      ЗАПАС РЕСУРСА

Теперь остается    выразить полный расход ресурса через выбранные неизвестные x1 и x2 . Так, расход ресурса первого вида на выпуск всех табуреток составит   4х1  единиц,  а  на  выпуск всех стульев   5х2 соответственно (см. первую строку таблицы). В сумме это даст полный расход ресурса  первого  вида  и  ограничение примет вид линейного неравенства

4х1 + 6х2 ≤ 24

Аналогично запишутся ограничения по второму и третьему видам ресурсов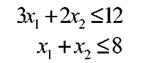

Объединяя их в систему получим

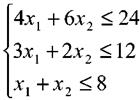
Далее, исходя из смысла введенных переменных, (число производимых изделий не может быть отрицательным) на них необходимо наложить ограничения неотрицательности.

Окончательно выпишем математическую модель задачи в форме ЗЛП.

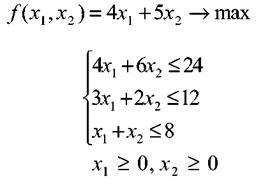
Полученная модель может изменяться за счет изменения, как условий производства, так и условий реализации продукции. Например, при изменении условий реализации изменятся и коэффициенты в целевой функции. При изменении запасов ресурсов изменятся правые части в системе ограничений. При учете новых условий производства система ограничений дополнится новыми уравнениями или неравенствами.

После решения поставленной ЗЛП переменные x1 и х 2 укажут плановое количество табуреток и стульев для получения максимальной прибыли, а разность между правой и левой частями каждого неравенства даст остаток ресурса каждого вида.