Эйлеровы и полуэйлеровы графы

Философ Иммануил Кант, гуляя по городу Кенигсбергу (сейчас этот город называется Калининград), поставил задачу (1736), известную в математике как задача о семи кенигсбергских мостах: можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз. Наш петербургский знаменитый математик швейцарского происхождения Леонард Эйлер блестяще решил эту задачу. На рис. 2 изображена схема семи мостов Кенигсберга (заметим, что сейчас осталось только два из них), а также мультиграф, соответствующий этой схеме (при построении графа считалось, что каждый берег реки и острова – это вершины графа, а мосты – его ребра; видно, что в данном случае у нас получился мультиграф без петель). Итак в Кенигсберге (ныне г. Калининград) течет река Неман. Она омывает два острова. Между берегами реки и островами во времена проживания в Кенигсберге Эйлера существовали 7 мостов, расположение которых показывает план на Рис. 4.1.

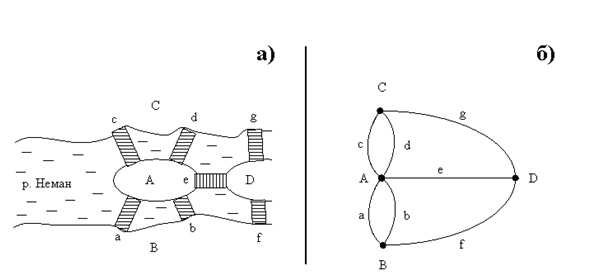
Задача Эйлера состояла в том, чтобы определить, можно ли выйдя из пункта С (или любого другого пункта) пройти каждый мост только по одному разу и вернуться в исходный пункт. Рассуждения и действия Эйлера в ходе решения этой задачи можно представить последовательностью следующих шагов: 1) он нарисовал план, 2) нарисовал неориентированный граф, ассоциированный с берегами, островами и мостами, 3) абстрагировал ассоциированный с данными граф от его содержания (см. Рис.4.1.б); это решающий шаг рассуждений Эйлера, поскольку абстрактный граф можно ассоциировать с чем угодно, например с площадями и улицами между ними, 4) сформулировал и доказал следующую теорему - Конечный граф G является эйлеровым графом тогда и только тогда, когда

а) Граф G связан

б) Все его локальные степени четные.

Поясним, что число ребер, инцидентных одной вершине графа, называется локальной степенью в этой вершине. Мы не будем доказывать эту теорему, которая является второй частью рассуждений Эйлера.

Любой граф может быть нарисован на бумаге или экране компьютера и представлен формально. Поэтому нарисованный на экране компьютера граф может быть транслирован в память компьютера. Покажем каким образом графы рисуются на бумаге и представляются формально на примере трех простейших графов, каждый из которых состоит из одного ребра. Они показаны на Рис. 4.2.

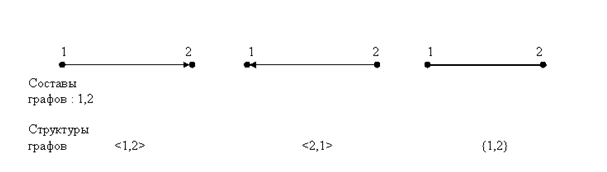
Рис. 4.2 раскрывает сущность теории графов в наглядной и формальной формах.

В соответствии с поставленной Кантом (и решенной Эйлером) задачей можно дать следующие определения:

Граф (или мультиграф без петель) называется эйлеровым, если существует цикл без повторения ребер (такой цикл называют эйлеровым), обходящий все вершины графа. Граф называется полуэйлеровым, если существует маршрут без повторения ребер (эйлеров путь), обходящий все ребра графа ровно один раз. На рис. 4.3 изображены: а – эйлеров граф, б – полуэйлеров граф и в – граф, не являющийся ни эйлеровым, ни полуэйлеровым (люди старшего поколения знают, что в школах раньше было много загадок типа “можно ли нарисовать данную фигуру не отрывая ручку от бумаги”, что и соответствует эйлерову или полуэйлерову графу).

Рис. 4.3.

Теорема (Эйлер). Для того чтобы данный связный граф (не орграф, но, возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными. Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными.

Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.

С точки зрения задачи о рукопожатиях это означает, что число гостей, которые поздоровались за руку нечетное число раз, должно быть четным.

Заметим, что все 4 вершины мультиграфа (рис. 2), соответствующего мостам Кенигсберга, имеют степень 3. Поэтому эйлеров цикл или путь невозможен.

Примечание. Если граф (или мультиграф без петель) содержит 2k вершин нечетной степени, то его можно разбить на k полуэйлеровых графов (т. е. нарисовать k росчерками пера).

Рассмотрим некоторые приложения теоремы Эйлера, которые в основном связаны с так называемой задачей китайского почтальона.

Пусть имеется некоторый граф (связный), ребрам которого приписаны некоторые числа, называемые весами ребер (часто, но не всегда!, в приложениях вес ребра – это его длина). Требуется найти такой цикл, при котором каждое ребро проходится, по крайней мере, один раз и суммарный вес всех ребер, вошедших в цикл, минимален. Заметим, что если граф является эйлеровым, то любой эйлеров цикл решает поставленную задачу (для эйлерова графа веса роли не играют).

Эта задача имеет много приложений, например, поливка улиц одной машиной (здесь ребра графа – дороги, а перекрестки – вершины; веса – это длины дорог), а также сбор мусора, доставка почты или даже наилучший маршрут для осмотра музея или уборка помещений и коридоров в больших учреждениях.

Заметим, что имеется алгоритм решения задачи китайского почтальона, но он требует достаточно длительного описания.

Кратко рассмотрим проблему, связанную с возможным обходом всех вершин в графе: существует ли в данном (связном) графе цикл (или маршрут), обходящий каждую вершину (кроме первой) только один раз. Если такой цикл (маршрут) существует (в этом случае такой цикл будет контуром, а маршрут – путем), то граф называется гамильтоновым (полугамильтоновым), и соответствующий цикл (путь) также называют гамильтоновым циклом (путем).

На рис. 4.4 изображены гамильтонов, полугамильтонов и не гамильтонов графы.

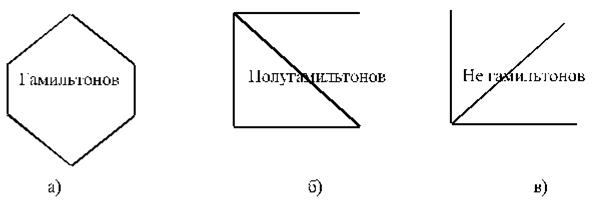
Рис. 4.4.

Несмотря на сходство постановки задач для гамильтоновых графов с эйлеровыми, “хорошего” решения для гамильтоновых графов нет. Вообще, о гамильтоновых графах известно очень мало. В основном – это теоремы типа “если в графе достаточное число ребер, то он гамильтонов”. Ясно, что теоремы такого типа не могут дать критерия гамильтонова графа, (рис. 6,а), поскольку в графах такого типа вершин может быть очень много, а ребер сравнительно мало).