Симметрия относительно прямой

Определение. Симметрией S относительно прямой  называется преобразование плоскости, при котором образом точки А является такая точка А' (этой же плоскости), что: 1) АА'; 2) точка А = АА'  — середина отрезка АА' (рис. 13).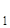

Прямая называется осью симметрии. Если точка К, то К'= К, т. е. каждая точка, принадлежащая , является двойной точкой преобразования симметрии;  других точек плоскости, обладающих этим свойством, нет. Докажем с помощью метода координат, что симметрия относительно прямой: 1) преобразует прямую в прямую; 2) сохраняет расстояние между точками.

Примем ось симметрии за ось ОХ прямоугольной декартовой системы координат. Тогда образом точки А(х; у) при этой симметрии служит точка А'(х; -у) (рис. 14). 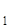Если прямая g определяется уравнением ах+ by + с= 0, то образом этой прямой будет множество точек {(х'; у')}, где х = х, у' = -у, определяемое уравнением ах - bу' + с = 0, т. е. некоторая прямая g'.

Пусть А (х; y), В(х; y) – две произвольные точки плоскости, а точки А' (х; -y), В' (х; -y) - их образы. Тогда

А'В'= .

Определение. Если при симметрии относительно прямой  некоторая фигура F отображается на себя, то прямая  называется осью симметрии этой фигуры.

Так каждый диаметр окружности является осью симметрии этой окружности; каждая прямая, перпендикулярная данной прямой, является осью симметрии этой прямой; каждая высота правильного треугольника является его осью симметрии.