Поворот

Определение. Пусть заданы точка О — центр поворота и некоторый ориентированный угол а. Тогда поворотом вокруг точки О на угол  называется преобразование, при котором каждой точке А плоскости ставится в соответствие такая точка А' этой плоскости, что: 1) ОА'=ОА; 2) угол АОМ конгруэнтен углу  и ориентирован так же, как угол . Поворот на угол  обозначается R.  С помощью метода координат можно убедиться, что при повороте прямая отображается на прямую и сохраняются расстояния между точками.

Выберем начало координат прямоугольной декартовой системы в центре поворота (рис. 11) и ориентируем угол () так же, как данный угол .

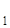
Пусть А (х; у)       А' (х'; у'). Если обозначить угол (,) через Р, то (рис. 15) угол (i, OA') будет иметь такую же величину, как и угол +. Поэтому

х' = ОА'  =ОА'cos (+) = ОА' (cos cos  - sin sin ).

          Аналогично

y' = ОА'  =ОА' sin (+) = ОА' (sincos + cossin).

          А так как ОАcos =х, ОАsin=y, то

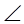              (2)

Решая уравнение системы (2) относительно х и y получим:

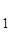
Значит, образом прямой ах+by+c=0 будет фигура, определяемая  уравнением

          Нетрудно проверить, что если при повороте АА', ВВ', то А'В'=АВ.