Определение. Поворот вокруг точки О на угол, величина которого равна 180°, называют симметрией относительно точки О или центральной симметрией. Точку О называют центром симметрии. 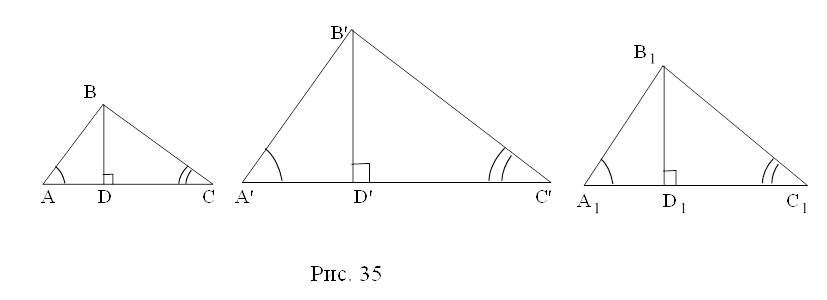
Ясно, что в этом преобразовании центр симметрии — точка О, а также точки А и А' (образ точки А) лежат на одной прямой (рис. 16) и ОА =OА'.
Определение. Если какая-либо фигура при симметрии относительно точки О отображается на себя, то точка О называется центром симметрии этой фигуры.
Так, центр окружности является одновременно и ее центром симметрии, точка пересечения диагоналей параллелограмма — центром симметрии этого параллелограмма.
Подобие
Определение. Преобразование плоскости называется подобием, если для любых двух точек А и В плоскости и их образов А' и В' имеет место соотношение: А'B'=kAB, где k – положительное число, называемое коэффициентом подобия,
Определение. Фигура Ф называется подобной фигуре Ф' (Ф ~ Ф'), если существует преобразование подобия, при котором фигура Ф преобразуется в фигуру Ф'.
Отметим некоторые важнейшие свойства преобразования подобия.
1. Преобразование подобия сохраняет коллинеарность точек, а также порядок расположения точек на прямой.
Действительно, если, например, точка В лежит между точками А и С, то AC=AB+BC. При этом, согласно определению подобия, для образов А', В', С' точек А, В, С мы получим следующее соотношение:
A'C'=kAC=k(AB+BC)=kAB+kBC=A'B'+B'C'.
Соотношение A'C'=A'B'+B'C' показывает, что точки A', B', C' лежат на одной прямой, причем точка В' лежит между точками А' и С'.
Из сохранения порядка точек вытекает также сохранение сорасположенности или противорасположенности двух точек относительно некоторой прямой.
2. Точки, не лежащие на одной прямой, преобразуются в точки, не лежащие на одной прямой. Действительно, в противном случае при обратном преобразовании нарушалась бы коллинеарность точек.
Из сказанного вытекает, что:
3. Подобие преобразует прямую в прямую, отрезок прямой – в отрезок, луч – в луч, угол – в угол, многоугольник - в одноименный многоугольник, окружность – в окружность.
4. Преобразование подобия сохраняет величину угла, т.е. является конформным преобразованием. В частности, при преобразовании подобия сохраняется перпендикулярность прямых.
5. При подобии многоугольник преобразуется в одноименный ему многоугольник, углы которого конгруэнтны соответственным углам, а стороны пропорциональны соответственным сторонам данного многоугольника.
Докажем теперь теорему существования подобия.
Теорема. Если стороны треугольника А'В'С' пропорциональны соответственным сторонам треугольника АВС, то существует и притом единственное преобразование подобия, преобразующее вершины А, В, С треугольника АВС соответственно в вершины А', В', С' треугольника А'В'С'.
1. Доказательство существования
Пусть АВС и А'В'С' – два треугольника, причем
A'B' : AB = A'C' : AC = B'C' : BC|= k.
Построим (рис. 17) на луче А'В' такую точку В", что A'B''=AB, и на луче А'С' такую точку С'', что A'C''=AC. Углы треугольника А'В'С' имеют те же величины, что и соответственные углы треугольника АВС. В частности, ![]() В'А'С'=
В'А'С'=![]() ВАС. А так как углы В'А'С' и В''А'С'' совпадают, то
ВАС. А так как углы В'А'С' и В''А'С'' совпадают, то ![]() В''А'С''=
В''А'С''=![]() ВАС.
ВАС.
Из соотношений A'B''=AB, A'C''=AC и ![]() В''А'С'=
В''А'С'=![]() ВАС следует, как известно, что B''C''=BC.
ВАС следует, как известно, что B''C''=BC.
Из соотношений A'B''=AB, A'C''=AC, B''C''=BC следует, что существует перемещение L преобразующее точки А, В, С, соответственно в точки А', В'', С''.
2. Доказательство единственности
Если точка М на прямой АВ, то точка М' – ее образ в подобии - однозначно определяется тем, что 1) М' ![]() А'В', 2)A'M'=kAM, 3) точки А', В', М' располагаются на прямой на прямой АВ.
А'В', 2)A'M'=kAM, 3) точки А', В', М' располагаются на прямой на прямой АВ.
Если же М![]() АВ, то ее образ однозначно определяется следующими условиями: 1)
АВ, то ее образ однозначно определяется следующими условиями: 1) ![]() В'А'М'=
В'А'М'=![]() ВАМ, 2) A'M'=kAM, 3) точка М' сорасположена или противорасположена с точкой С' относительно прямой А'В' соответственно тому, сорасположена ли или противорасположена точка М с точкой С относительно прямой АВ.
ВАМ, 2) A'M'=kAM, 3) точка М' сорасположена или противорасположена с точкой С' относительно прямой А'В' соответственно тому, сорасположена ли или противорасположена точка М с точкой С относительно прямой АВ.
Поможем написать любую работу на аналогичную тему

