Простейшие задачи на построение

Набор простейших задач на построение в различных пособиях для школы примерно одинаков, хотя порядок рассмотрения этих задач может быть различным.

К простейшим обычно относятся следующие задачи на построение:

1) Построение угла, равного данному;

2)    Построение биссектрисы угла;

3)    Деление отрезка пополам;

4)    Построение прямой, проходящей через данную точку и перпендикулярной данной прямой.

Эти задачи изучаются в 7 классе – глава II «Треугольники». На изучение данной темы отводится 3 часа. В результате изучения ученики должны научиться решать задачи на построение с помощью циркуля и линейки, уметь доказывать правильность выполняемых операций.

На первом уроке предлагается рассмотреть задачи: построение угла равного данному и построение биссектрисы угла. Второй урок посвящен решению задач: деление отрезка пополам и построение перпендикулярных прямых. Третий урок – решение задач, отрабатывающих умения и навыки построения циркулем и линейкой.

Первоначально учителю необходимо выявить систему условий, на которую должен опираться ученик для успешного овладения практическим действием.

Для того чтобы научиться производить построения с помощью циркуля и линейки, ученикам необходимо иметь знания о следующих фактах: о данных геометрических фигурах – полупрямой, полуплоскости и угле, отрезке, биссектрисе, перпендикуляре (определения, представления об их изображении и обозначении); о цели действия; об инструментах построения; о каждой из конструктивных операций и о последовательности их выполнения. Учащиеся должны быть также подготовлены к обоснованиям возможности каждого шага построения и доказательству правильности построения (аксиомы откладывания отрезков и углов, определение равных треугольников, признаки равенства треугольников). Нельзя обойтись и без навыков в выполнении элементарных конструктивных операций: построение окружности произвольного или указанного радиуса с центром в некоторой точке, построение полупрямой, имеющей данное начало и проходящей через данную точку.

Рассмотрим несколько уроков изучения нового материала темы «Задачи на построение».

Урок№1

Тема: Построение угла, равного данному. Построение биссектрисы угла

Цели: 1. Познакомить учащихся с задачами на построение, при решении которых, используются только циркуль и линейка.

2. Научить выполнять построение угла, равного данному, строить биссектрису угла.

3. Развитие пространственного мышления, внимания.

4. Воспитание трудолюбия и аккуратности.

Оборудование: таблицы с порядком решения задач на построение.

Ход урока:

Актуализация основных теоретических понятий: окружность, заданного радиуса с данным центром; признаки равенства треугольников; через две точки на плоскости можно провести прямую и притом только одну.

Для повторения признаков равенства треугольников можно предложить задание: укажите на каком из рисунков (рис. 18) есть равные треугольники.

Повторение понятия окружности и ее элементов можно организовать, предложив классу следующее задание, с выполнением его одним учеником на доске: дана прямая а и точка А, лежащая на прямой и точка В, не лежащая на прямой. Провести окружность с центром в точке А, проходящую через точку В. Отметьте точки пересечения окружности с прямой а. Назовите радиусы окружности.

Для рассмотрения нового материала учителю полезно иметь таблицу. (табл. 1). Работу с таблицей можно организовать по-разному: она может иллюстрировать рассказ учителя или образец записи решения; можно предложить учащимся, пользуясь таблицей, рассказать о решении задачи, а затем самостоятельно его выполнить в тетрадях. Таблица может быть использована при опросе учащихся и при повторении материала. 

Учащимся можно предложить в указанном порядке составить план решения задачи.

                                                                                                  Таблица 1.

 Построение биссектрисы данного угла

Учитель может предложить учащимся по данной  таблице построить биссектрису угла.

Ученик у доски выполняет построение, обосновывая каждый шаг выполняемых действий.

          Доказательство показывает учитель, необходимо подробно остановиться на доказательстве того факта, что в результате построения действительно получатся равные углы.

                                                 Закрепление

Полезно предложить учащимся следующее задание для закрепления пройденного материала:

Задача 1. Дан тупой угол АОВ. Постройте луч ОХ так чтобы углы ХОА и ХОВ были равными тупыми углами.

Задача 2. Построить с помощью циркуля и линейки углы в 30º и 60º .

Задача 3. Постройте треугольник по стороне, углу, прилежащему к его стороне, и биссектрисе треугольника, исходящей из вершины данного угла.

                                                                                                            Таблица 2.

Для домашней работы: №150-152.                                      

          Урок№2

Тема: Построение середины отрезка.Построение перпендикулярных прямых

Цель: 1. Научить учащихся с помощью циркуля и линейки выполнять деление отрезка пополам.

2. Сформировать умения и навыки построения перпендикулярных прямых.

3. Актуализация внимания.

4. Воспитание трудолюбия и аккуратности.

Ход урока:

Методом фронтального опроса повторить понятия: окружность заданного радиуса с данным центром, признаки равенства треугольников, свойства равнобедренного и равностороннего треугольников.

Далее предложить задание: с помощью циркуля и линейки построить биссектрису, выходящую из вершины равнобедренного треугольника. Перечислить ее свойства.

При изучении нового материала используется таблица 3, по которой учащиеся составляют рассказ, как разделить данный отрезок пополам. После этого в тетрадях выполняются соответствующие построения.

Таблица 3

Построение перпендикулярных прямых

Здесь необходимо обратить внимание, что возможны два случая:

1.    Точка принадлежит прямой;

2.    Точка не принадлежит прямой.

После повторения учитель формулирует задачу и объясняет построение для первого случая, при этом может быть использована таблица 4.

          При рассмотрении второго случая учащиеся при помощи таблицы 4 проводят построение и доказательство самостоятельно.     

                                       Таблица 4

Закрепление

Задача.  Постройте прямоугольный треугольник по его катетам.

Данную задачу ученик решает у доски, предварительно проведя ее анализ. Запись решения данной задачи может выглядеть так:

ДОКАЗАТЕЛЬСТВО:

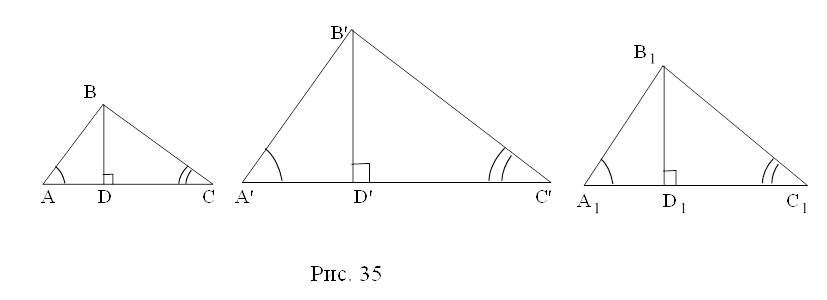
В АВС ВС=а, СА= b, ВDАС, следовательно, угол ВСА равен 90º . Значит треугольник АВС – искомый.

          Также для отработки умений и навыков, можно использовать задачи №154 (а,б).

          Для домашней работы: №153.

          Урок№3

Тема:  Решение задач на построение

Цель: 1. Отработка умений и навыков выполнения элементарных построений с помощью циркуля и линейки.

2.Актуализация внимания.

Ход урока:

          Проверить выполнение задачи №153. Проверку можно организовать так: у доски три ученика, они должны построить прямую, проходящую через

точку А перпендикулярно прямой 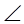а.

          Класс в это время может выполнить задание: дан треугольник АВС. построить высоту АD. После выполнения задания каждый шаг построения должен быть прокомментирован и обоснован.

          Самостоятельная работа.

1.    Разделить отрезок на 4 равные части.

2.    Дан АВС. Построить биссектрису ВК.

3.    Дан угол АОВ. Построить угол, для которого луч ОВ является биссектрисой.