Геометрическое место точек - Методика обучения решению задач на построение

Работающим по учебнику Л. С. Атанасяна можно предложить рассмотреть на факультативных занятиях следующие темы: «Геометрическое место точек», «Метод геометрических мест».

            Этот урок можно начать с рассказа учителя. Приведем его примерное содержание.

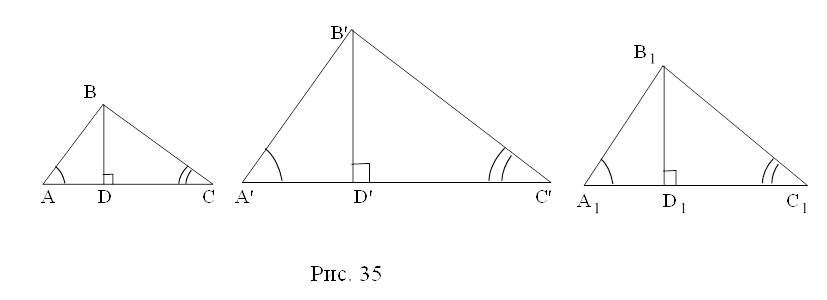
            На плоскости часто приходится рассматривать точки, которые обладают одним и тем же свойством, например: удаленные от данной точки О на расстояние 10 см, или удаленные от данной прямой а на 15 см, или одинаково удаленные от концов данного отрезка АВ и т.д. По ходу объяснения на доске открываются рисунки (рис. 23).

Рассматривая такие точки, выделяют фигуры, которые состоят из всех точек плоскости, обладающим некоторым свойством.

Сначала объясняется слово «состоит». Фигура состоит из точек, обладающих определенным свойством, это значит, что каждая точка фигуры обладает этим свойством или иначе, если точка принадлежит фигуре, то она обладает данным свойством. Затем объясняются слова: «состоит из всех точек плоскости». Фигура может состоять из всех точек плоскости, обладающих определенным свойством, но не включать все точки плоскости с данным свойством. Когда же говорят, что фигура состоит из всех точек плоскости с данным свойством, то это означает не только, что каждая точка фигуры обладает этим свойством, но и что каждая точка плоскости, обладающая данным свойством, принадлежит данной фигуре, или иначе, если точка плоскости обладает данным свойством, то она принадлежит данной фигуре.

            Делая вывод, что слова «фигура состоит из всех точек плоскости, обладающих определенным свойством» означают:

            1. Если точка принадлежит фигуре, то она обладает данным свойством.

            2. Если точка обладает данным свойством, то она принадлежит фигуре.

            Эти два условия – взаимно обратные утверждения. Разъясним сказанное на примере. Рассмотрим три фигуры: окружность, часть окружности и фигуру, состоящую из окружности и точек заштрихованной части плоскости (табл. 5). (Рисунок помещен в таблице, на которой знаки «+», «-», ГМТ пока не проставлены. Это будет сделано в процессе дальнейшей беседы с классом.)

            Учитель обращает внимание учащихся на то, что будут рассматриваться точки плоскости со свойством: точки удалены от данной точки О на расстояние, равное R. Классу предлагается выяснить, для каких из данных трех фигур выполняются два указанных выше условия, т.е. какая из трех фигур состоит из всех точек плоскости, удаленных от точки О на расстояние, равное R.

            Заполняется таблица (ставятся знаки «+», «-»). Необходимо объяснить, почему для второй фигуры не выполняется второе условие (фигуре принадлежат не все точки с указанным свойством); почему для третьей фигуры не выполняется первое условие (фигуре принадлежат и точки, не обладающие указанным свойством).

Заполнив таблицу учащиеся должны сделать вывод какая из фигур удовлетворяет двум поставленным условиям и дать определение геометрического места точек.

          Задание. Приведите примеры точек, так же удовлетворяющих поставленным условиям ГМТ (серединный перпендикуляр, биссектриса угла).

Закрепление

1. Верно ли утверждение, что отрезок АВ, параллельный данной прямой а и удаленный от нее на 5 см, является геометрическим местом точек, удаленных от данной прямой на 5 см?

Условие задачи можно варьировать: взять два отрезка, отрезок и прямую и, наконец, две прямые (рис. 24).

2. Можно ли прямую АВ, где А и В – различные точки прямой, считать геометрическим местом точек, лежащих между точками А и В?

Затем в условиях данной задачи заменяется прямая лучом АВ, а луч отрезком АВ.

3. Можно ли отрезок АВ, параллельный двум параллельным прямым а и b и одинаково отстоящий от них, считать геометрическим местом точек, одинаково удаленных от двух параллельных прямых?

          Рис. 24

4. Найдите геометрическое место точек, одинаково удаленных от двух параллельных прямых а и b.

Решение. Проведем общий перпендикуляр DM прямых а и b и найдем его середину N (рис. 25). Через точку N проведем прямую m, параллельную прямой а (она будет параллельна и прямой b). Докажем, что прямая m есть искомое геометрическое место точек.

Доказательство. 1) Докажем, что если точка К принадлежит прямой m, то она удалена от прямых а и b на расстояние, равное р, где р-длина отрезка DN или MN. Так как параллельные прямые равноотстоящие, то точка К удалена как от прямой а, так и от прямой b на расстояние, равное р.                                                     

          2) Докажем, что точка S, одинаково удаленная от прямых а и b, принадлежит прямой m. Так как расстояние между прямыми а и b равно 2р, то точка S середина отрезка СЕ, перпендикулярного к прямым а и b и равного 2р. Пусть Sm, а СЕ пересекает m в точке R. Тогда RC=RE=p по доказанному в первой части, т.е. отрезок СЕ имеет две середины R и S, что невозможно, значит, Sm.