Тема «Движение», представленная в учебниках по геометрии для основной школы, содержит немного задач на применение преобразований фигур. Однако по данной теме можно найти интересные геометрические задачи. Они могут быть разнообразны и по уровню сложности, и по учебному материалу, необходимому для решения. Это разнообразие можно с успехом использовать в ходе повторения темы «Движение». Опишем один урок повторения. Он начинается с того, что учащиеся повторяют определения и построения, относящиеся к центральной симметрии, осевой симметрии, повороту, параллельному переносу. Для этого предлагаются следующие задания; которые выполняются у доски:
1) Построить отрезок, симметричный относительно прямой; точки.
2) Выполнить параллельный перенос треугольника на заданный вектор.
3) Построить прямую, которая получается из заданной прямой поворотом вокруг точки О на угол 80º по часовой стрелке.
После повторения теоретической части предлагаются задачи на построение, которые предлагается решать учащимися у доски.
Задача1. Построить параллелограмм по двум противоположным вершинам, лежащим на сторонах данного четырехугольника, причем остальные вершины параллелограмма также должны принадлежать сторонам данного четырехугольника.
Решение. 1. Анализ. Пусть искомый параллелограмм построен. На рис. 30а, это параллелограмм АВСD, который вписан в данный четырехугольник LMNK, точки В и D – данные.
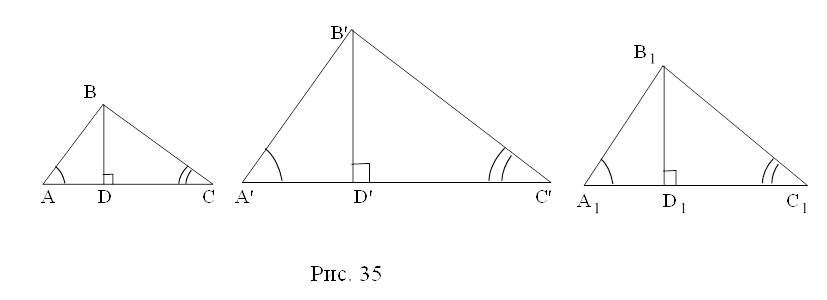
Проанализируем, что можно предпринять, чтобы стала видна возможность построения. Пока видно только одно: можно провести диагонали. Проводим диагонали BD и СА ( рис. 30б) и тут же замечаем, что точка О их пересечения является центром симметрии параллелограмма. А это значит, что она лежит на пересечении отрезка ML с образом отрезка KN при симметрии относительно точки О. Таким образом, мы нашли способ построения третьей вершины искомого параллелограмма. А четвертую его вершину можно найти, исходя из свойств этой фигуры.
2. Построение. Проведем отрезок BD и разделим его пополам точкой О.
Строим точки K
и N, симметричные относительно О точкам K и N соответственно.
Обозначим через А точку пересечения отрезков ML и KN. Строим точку С, симметричную относительно О точке А. Искомая фигура – АВСD (рис. 31).
3. Доказательство. Точки А и С, В и D – симметричны относительно точки О по построению. А это значит, что диагонали BD и АС четырехугольника АВСD пересекаются и точкой пересечения делятся пополам. Отсюда следует (по определению), что построенный четырехугольник - параллелограмм.
4. Исследование. Успех построения зависит от возможности найти точку А.
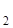Если прямые KN и LM пересекаются, то пересекаются и прямые KN, LM. Тогда задача имеет единственное решение. Это значит, что данный четырехугольник не должен быть ни параллелограммом, ни трапецией с основаниями KN и ML.
Есть и еще одно ограничение. Стороны KN и ML должны быть такими, чтобы пересекались отрезки KN и ML. Иначе пересечение прямых ML и KN вне отрезка ML привело бы к видоизменению задачи.
Если KN÷ïLM, то задача имеет либо множество решений (когда прямые MN и KN оказываются параллельными).
Задача 2. Точки А и В лежат по разные стороны от прямой d. Постройте на ней такую точку Х, чтобы биссектриса угла АХВ лежала на прямой d.
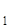Решение. 1. Анализ. Предположим, что точка Х найдена (рис. 32). Тогда ÐАХЕ=ÐЕХВ. А это значит, что лучи АХ и ВХ симметричны относительно луча ХЕ. Проведем перпендикуляры к прямой d из точек А и В. они пересекут лучи угла АХВ в точках А и В соответственно. Причем точки А и А, В и В симметричны друг другу относительно прямой d.
2. Построение. Строим точку А, симметричную точке А относительно прямой d.
Строим точку В, симметричную точке В относительно прямой d.
Точки А и В (А, В) оказались в одной полуплоскости, а прямые ВА и ВА пересекаются в искомой точке Х.
3. Доказательство. Углы АХЕ и ВХЕ равны по построению, следовательно, ХЕ – биссектриса, но луч ХЕ принадлежит прямой d. Значит, точка Х искомая.
4. Исследование. Если точка А
совпадает с точкой В, то возможно только одно решение.
Если точка А совпадает с точкой В, то задача имеет бесконечно много решений, так как любая точка прямой d удовлетворяет условию.
Если отрезок АВ оказывается параллельным прямой d, то решений нет.
Задача 3. Постройте такой равносторонний треугольник, чтобы одна его вершина совпадала с данной точкой О, а две другие принадлежали двум данным окружностям.
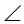
Решение. 1. Анализ. Предположим, что требуемый треугольник построен. Угол при данной вершине О равен 60°, причем ОА=ОВ. Это значит, что при повороте на 60° вокруг точки О против часовой стрелки вершина А перейдет в вершину В. значит, вторая искомая вершина треугольника является точкой пересечения образа окружности с центром О (при повороте на 60° вокруг точки О) с данной окружностью, имеющей центр О
.
2. Построение. Построим образ одной из окружностей при повороте на угол 60° с центром в данной точке О. Точка пересечения полученной окружности и второй из данных окружностей является второй вершиной треугольника. На рис. 33 это точка В.
Доказательство и исследование учащиеся должны провести дома самостоятельно.
Задача 4. Построить трапецию по диагоналям d, d и двум параллельным сторонам а и b.
Решение. 1. Анализ. Предположим, что искомая трапеция построена и в ней проведены диагонали d и d. Попробуем построить фигуру, в которой диагонали присутствовали бы в «целом» виде, т.е. без пересечения друг с другом. Оставим одну диагональ на месте, а другую (допустим, АС) перенесем параллельно на расстояние АD (рис. 34а). Получим треугольник ВЕD в котором известны три стороны:
ВЕ=а+b, BD= d, DE= d.
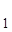
Точки В, Е, D позволяют построить параллелограмм АСЕD, в котором диагональ СD служит стороной искомой трапеции.
Для того чтобы найти другую сторону трапеции (рис. 34б), построим сначала треугольник АСЕ, у которого сторона АЕ является образом при параллельном переносе диагонали ВD на расстояние АD.
При таком анализе построение оказывается совершенно очевидным. Поэтому все последующие этапы решения целесообразно оставить учащимся для домашней работы.
Поможем написать любую работу на аналогичную тему