При решении многих задач на построение применяется метод подобия. Суть которого заключается в следующем: сначала строится фигура подобная данной, затем эта фигура увеличивается (уменьшается) в нужном отношении (т.е. строится подобная фигура), удовлетворяющая условию задачи.
Процесс обучения применению подобия к решению задач на построение целесообразно разбить на четыре этапа: подготовительный, ознакомительный, формирующий умение, совершенствующий умение. Каждый этап имеет свою дидактическую цель, которая достигается, когда учащиеся выполняют специально составленные задания.
Дидактическая цель подготовительного этапа – сформировать у учащихся умения: выделять данные, определяющие форму фигуры, множество пар подобных между собой фигур; строить фигуру по данным, определяющим форму; переходить от построенной фигуры к искомой.
После изучения первого признака подобия треугольников можно предложить следующий набор заданий:
Постройте треугольник по двум углам. Сколько решений имеет задача? Какие элементы определяют форму построенных треугольников?
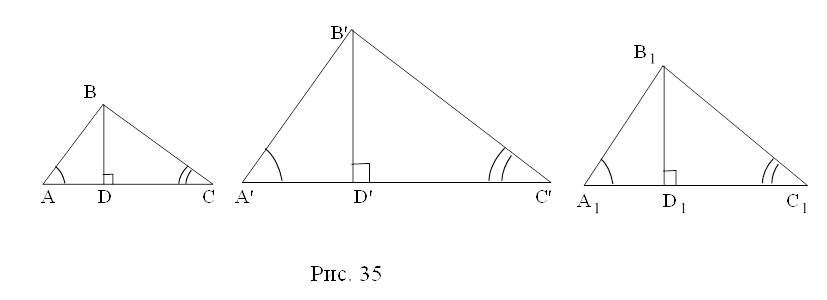
Назовите подобные треугольники на рис.35.
Известны следующие элементы треугольника: а) углы в 75°и 25°; б) высота 1,5 см; в) углы в 75° и 25°, высота 1,5 см. какие из этих данных определяют единственную фигуру на рис.35?
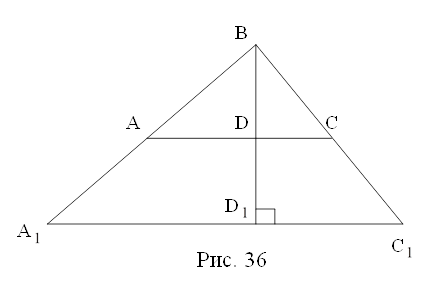
Подобны ли треугольники АВС и А![]() ВС
ВС![]() на рис.36, если АС÷ïА
на рис.36, если АС÷ïА![]() С
С![]() ? если они подобны, то каков их коэффициент подобия?
? если они подобны, то каков их коэффициент подобия?
Какие углы определяют форму треугольников на рис.36?
Можно ли будет определить размеры одного из треугольников на рис.36, если станут известны следующие данные: а) углы при основании треугольника; б) высоты треугольника; в) сторона и углы при основании?
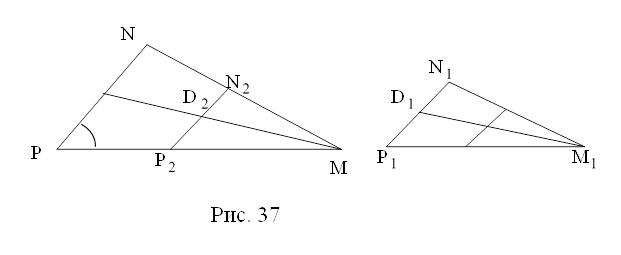
На рис.31 равные углы помечены одинаково. Кроме того, N![]() Р
Р![]() =N
=N![]() P
P![]() , М
, М![]() Р
Р![]() =МР
=МР![]() . Как расположены прямые NP и N
. Как расположены прямые NP и N![]() P
P![]() ?
?
Каким отношением связаны треугольники M![]() N
N![]() P
P![]() и MN
и MN![]() P
P![]() и их биссектрисы?
и их биссектрисы?
 Набор заданий, предъявляемых учащимся после изучения 2 и 3 признаков подобия треугольников, составляются аналогично. Однако при переходе от данного признака к следующему вопросы несколько усложняются, а именно: расположение треугольников на рисунках меняется, удаляясь от стандартного, варьируется набор элемента, определяющего единственную фигуру. Задания, например, могут быть такими:
Набор заданий, предъявляемых учащимся после изучения 2 и 3 признаков подобия треугольников, составляются аналогично. Однако при переходе от данного признака к следующему вопросы несколько усложняются, а именно: расположение треугольников на рисунках меняется, удаляясь от стандартного, варьируется набор элемента, определяющего единственную фигуру. Задания, например, могут быть такими:
1.  Подобны ли треугольники АВС и А
Подобны ли треугольники АВС и А![]() В
В![]() С
С![]() , если: а) АВ=5см, ВС=7см,
, если: а) АВ=5см, ВС=7см,
![]() В=30º, А
В=30º, А![]() В
В![]() =10см, В
=10см, В![]() С
С![]() =14см,
=14см, ![]() В
В![]() =60º; б) АВ=5см, ВС=7см,
=60º; б) АВ=5см, ВС=7см, ![]() В=30º, А
В=30º, А![]() В
В![]() =10см, В
=10см, В![]() С
С![]() =14см,
=14см, ![]() В
В![]() =30º; в) АВ=3см, ВС=5см, СА=7см, А
=30º; в) АВ=3см, ВС=5см, СА=7см, А![]() В
В![]() =4,5см, В
=4,5см, В![]() С
С![]() =7,5см, С
=7,5см, С![]() А
А![]() =10,5см; г) АВ=1,7см, ВС=3см, СА=4,2см, А
=10,5см; г) АВ=1,7см, ВС=3см, СА=4,2см, А![]() В
В![]() =34дм, В
=34дм, В![]() С
С![]() =60дм, С
=60дм, С![]() А
А![]() =84дм?
=84дм?
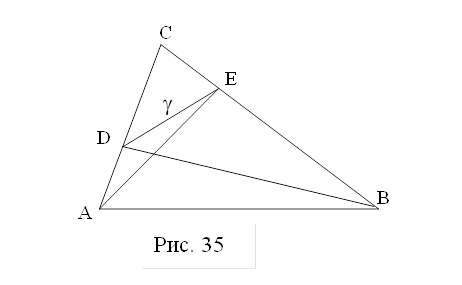
 2. В треугольнике АВС с острым углом С проведены высоты АЕ и ВD (рис. 35). Докажите, что
2. В треугольнике АВС с острым углом С проведены высоты АЕ и ВD (рис. 35). Докажите, что ![]() АВС подобен
АВС подобен ![]() ЕDC.
ЕDC.
3. Докажите, что у подобных треугольников периметры относятся как соответствующие стороны.
Дидактическая цель ознакомительного этапа в том, чтобы разъяснить учащимся структуру процесса построения методом подобия.
Объяснение начинается с задачи.
Задача 1. Построить треугольник по двум данным углам ![]()
![]() и
и ![]() и биссектрисе длины d, проведенной из вершины третьего угла.
и биссектрисе длины d, проведенной из вершины третьего угла.
Анализируя задачу с учащимися, учитель предлагает задания – вопросы, ответы на которые кратко фиксируются на доске. Вопросы могут быть такими:
1. Какие данные определяют форму искомого треугольника?
2. Какие данные определяют размеры искомого треугольника?
3. Сколько треугольников можно построить построение двум углам? Какими будут построение форме все построенные треугольники?
4. Какой отрезок нужно провести в треугольнике, подобном искомому?
5. Как построить искомый треугольник?
Ответы на вопросы сопровождаются выполнением на доске чертежа от руки (рис. 38).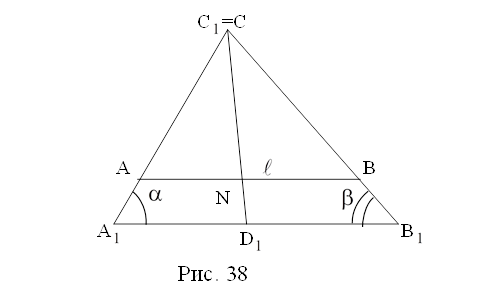
Далее составляется план построения и выполняется само построение. Запись построения у учащихся в тетрадях может быть такой:
а) D А![]() В
В![]() С
С![]() : ÐА
: ÐА![]() =
=![]() , ÐВ
, ÐВ![]() =
=![]() ;
;
б) построить биссектрису угла С![]() в треугольнике А
в треугольнике А![]() В
В![]() С
С![]() ,
,
в) построить С![]() N=d, N
N=d, N![]() C
C![]() D
D![]() ;
;
г) через точку N провести прямую ![]() ,
, ![]() ÷ï А
÷ï А![]() В
В![]() ;
;
д) ![]()
![]() А
А![]() C
C![]() =А,
=А, ![]()
![]() В
В![]() С
С![]() =В;
=В;
е) DАВС – искомый: ÐА=![]() , ÐВ=
, ÐВ=![]() (так как DАВС¥D А
(так как DАВС¥D А![]() В
В![]() С
С![]() по 1 признаку) и С
по 1 признаку) и С![]() N=d по построению. Дидактическая цель этапа, формирующего умение решать задачи рассматриваемого вида, ясна уже из его названия. Основная форма деятельности на этом этапе – индивидуально-поисковая. Она завершается обобщающей беседой.
N=d по построению. Дидактическая цель этапа, формирующего умение решать задачи рассматриваемого вида, ясна уже из его названия. Основная форма деятельности на этом этапе – индивидуально-поисковая. Она завершается обобщающей беседой.
Приведем несколько примеров задач, которые можно предложить на данном этапе.
Задача. Внутри угла АОВ задана точка F. Построить на стороне ОА точку М, одинаково удаленную от F и от стороны ОВ
Решение. 1. Анализ. Обратимся к рисунку 39. Пусть точка М построена, тогда MF=MP. Это означает, что искомая точка М – есть центр окружности g радиуса МF с центром М, касающуюся стороны ОВ в точке Р.
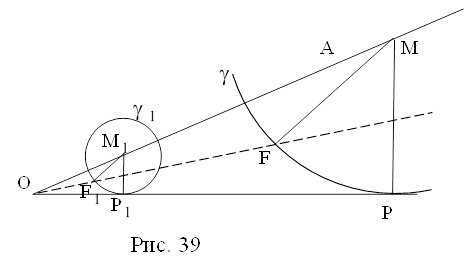 Если мы возьмем на ОА произвольную точку М и опустим ^М
Если мы возьмем на ОА произвольную точку М и опустим ^М![]() Р
Р![]() на СВ и найдем F
на СВ и найдем F![]() пересечения окружности g с центром М
пересечения окружности g с центром М![]() радиуса М
радиуса М![]() Р
Р![]() с прямой ОF, то DМ
с прямой ОF, то DМ![]() F
F![]() P
P![]() будет подобен DМFР. Отсюда вытекает требуемое построение.
будет подобен DМFР. Отсюда вытекает требуемое построение.
2. Построение. Проводим ОF, берем на СА произвольную точку М![]() и опускаем ^М
и опускаем ^М![]() Р
Р![]() на СВ. Проводим окружность g
на СВ. Проводим окружность g![]() радиуса М
радиуса М![]() Р
Р![]() с центром в точке М
с центром в точке М![]() . Пусть F
. Пусть F![]() - точка пересечения этой окружности с ОF. Проводим F
- точка пересечения этой окружности с ОF. Проводим F![]() M
M![]() и затем проводим прямую через точку F÷ïF
и затем проводим прямую через точку F÷ïF![]() M
M![]() . Точка М пересечения этой прямой с ОА – искомая.
. Точка М пересечения этой прямой с ОА – искомая.
3. Доказательство. Очевидно из проведенного анализа.
4. Исследование. Задача имеет 2 решения. Это следует из того, что окружность пересекается с ОF в 2-х точках.
Задача. Построить треугольник по 2 углам и периметру.
Решение. 1. Анализ. Пусть ![]() и y - данные углы и Р – периметр искомого треугольника (рис.40). Допустим, что искомый треугольник построен,
и y - данные углы и Р – периметр искомого треугольника (рис.40). Допустим, что искомый треугольник построен,
тогда, если мы рассмотрим какой-либо DАВ![]() С
С![]() , подобный искомому, отношение периметра Р DАВС к периметру Р
, подобный искомому, отношение периметра Р DАВС к периметру Р![]() DАВ
DАВ![]() С
С![]() равно отношению сторон
равно отношению сторон
АС и АС![]() .
.
2. Построение. Построим DАВС подобный искомому. На луче АВ, отложим отрезки АD=Р и АD![]() =Р
=Р![]() , затем соединим точку D
, затем соединим точку D![]() и С
и С![]() , и через точку D проведем прямую ÷ï D
, и через точку D проведем прямую ÷ï D![]() C
C![]() .
.
Пусть С – точка пересечения прямой с лучом АС![]() . Через точку С проведем прямую ÷ï С
. Через точку С проведем прямую ÷ï С![]() В
В![]() и обозначим В точку пересечения этой прямой с AD, тогда DАВС – искомый.
и обозначим В точку пересечения этой прямой с AD, тогда DАВС – искомый.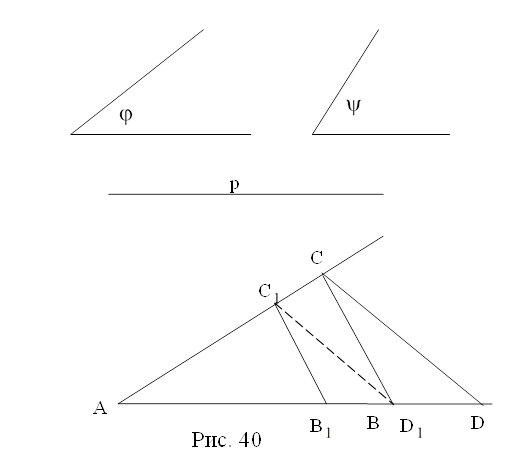
3. Доказательство. Очевидно, что DAС![]() D подобен DАСD, поэтому
D подобен DАСD, поэтому 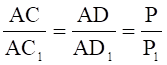 . По соотношению сторон
. По соотношению сторон 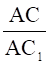 равно отношению периметров подобных DАВС и DАВ
равно отношению периметров подобных DАВС и DАВ![]() С
С![]() , поэтому периметр DАВС=Р, следовательно, DАВС – искомый.
, поэтому периметр DАВС=Р, следовательно, DАВС – искомый.
4. Исследование. Так как сумма любых двух углов треугольника <180°, то условие ![]() +y<180° является необходимым условием для данного построения оно и достаточно. Затем указанным выше способом строится искомый DАВС. Такой треугольник единственный, ибо любой другой с такими же данными будет иметь периметр Р и следовательно, будет подобен построенному с коэффициентом подобия равным 1, а два подобных треугольника с одним коэффициентом равны.
+y<180° является необходимым условием для данного построения оно и достаточно. Затем указанным выше способом строится искомый DАВС. Такой треугольник единственный, ибо любой другой с такими же данными будет иметь периметр Р и следовательно, будет подобен построенному с коэффициентом подобия равным 1, а два подобных треугольника с одним коэффициентом равны.
Задача. Дан ÐАОВ и точка М, расположенная во внутренней области этого угла. Построить окружность g, проходящую через точку А касающуюся сторон угла АОВ.
Решение. 1. Анализ. Пусть ÐАОВ – данный и точка М, расположена во внутренней области угла (рис. 41). Проведем еще одну окружность g, касающуюся сторон ÐАОВ. Обозначим, М![]() - точку пересечения окружности g с прямой ОМ и рассмотрим DОМN и ОМ
- точку пересечения окружности g с прямой ОМ и рассмотрим DОМN и ОМ![]() N
N![]() (N и N
(N и N![]() центры окружности g и g
центры окружности g и g![]() ). Эти треугольники подобны по двум углам, поэтому построение искомой окружность можно провести следующим образом:
). Эти треугольники подобны по двум углам, поэтому построение искомой окружность можно провести следующим образом:
2. Построение. Так как центр искомой окружности лежит на биссектрисе ÐАОВ, то проводим биссектрису угла. Далее, возьмем здесь же точку N![]() и построим окружность g
и построим окружность g![]() с центром N
с центром N![]() , касающуюся
, касающуюся
ÐАОВ. Затем проводим прямую СМ и обозначим через М![]() - точку пересечения прямой с окружностью (таких точек две - М
- точку пересечения прямой с окружностью (таких точек две - М![]() и М
и М![]() - берем одну из них). Проводим прямую М
- берем одну из них). Проводим прямую М![]() N
N![]() и ÷ïей прямую через точку М. Тогда N -пересечение прямой с биссектрисой угла и есть центр искомой окружности, а ее радиус равен МN. Проведем ее.
и ÷ïей прямую через точку М. Тогда N -пересечение прямой с биссектрисой угла и есть центр искомой окружности, а ее радиус равен МN. Проведем ее.
3. Доказательство. По построению окружность g подобна g![]() , О – центр подобия. Это следует из подобия треугольников ОМN и ОМ
, О – центр подобия. Это следует из подобия треугольников ОМN и ОМ![]() N
N![]() ,поэтому раз окружность g касается сторон угла, то и окружность g
,поэтому раз окружность g касается сторон угла, то и окружность g![]() будет касаться сторон угла .
будет касаться сторон угла .
4. Исследование. Задача имеет два решения, т.к. ОМ пересекается с окружностью g![]() в двух точках М
в двух точках М![]() и М
и М![]() , каждой из которых будет соответствовать своя окружность, проходящая через точку М и
, каждой из которых будет соответствовать своя окружность, проходящая через точку М и
касающаяся сторон ÐАОВ.
Дидактической целью этапа, совершенствующего умение решать задачи типа рассмотренных, является перенос сформированного умения на более сложные задачи, в частности на следующие ситуации: искомая фигура занимает определенное положение по отношению к данным точкам или линиям, при этом устранение одного из условий задачи приводит к системе подобных или гомотетичных фигур. Приведем пример такой задачи.
Задача. В данный треугольник впишите квадрат так, чтобы две его вершины лежали на одной стороне треугольника, а две другие – на двух других сторонах.
Задачи, соответствующие целям этого этапа, исключены из числа задач обязательного уровня. Поэтому они предлагаются только хорошо успевающим школьникам. Главное внимание на этом этапе уделяется индивидуально-поисковой деятельности учащихся.
Поможем написать любую работу на аналогичную тему

