Охарактеризуйте сущность и цель корреляционного анализа. Коэффициент корреляции и диапазоны его значения.

Любые значимые исследования обычно подкрепляются достоверными империческими данными. Политологам нередко приходится обращаться к готовым социологическим исследованиям, статистике. Статистика позволяет решать множество разнообразных задач, обрабатывать большие массивы информации, может являться «иллюстрацией» к политологическим разработкам.

Корреляционный и факторный виды анализа относятся к статистическим методам, используемых в политической науке. Попробуем провести сравнительное исследование двух методов, найти общее и особенное. Для этого определим цели данных видов анализа, определим когда используется тот или иной вид анализа, какие выводы позволяет сделать каждый из методов.

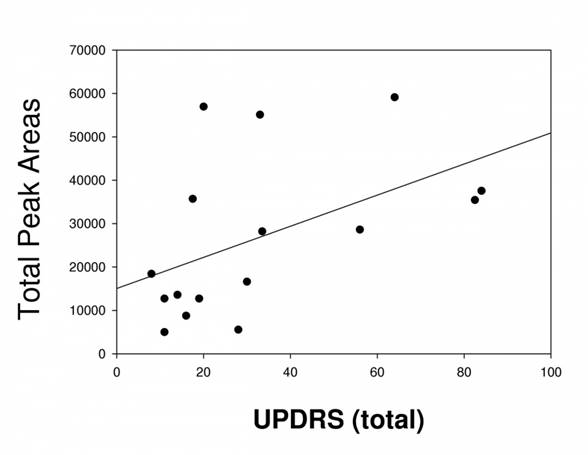
Корреляционный анализ является одним из наиболее широко используемых статистических методов в политической науке, часто осуществляется как составная часть более сложных, комплексных методов (в том числе факторного анализа). Целью корреляционного анализа является измерение статистической взаимозависимости между двумя или более переменными. Важно, что переменные в корреляционном анализе не делятся на зависимые и независимые. Исследуется именно взаимозависимость переменных, а не влияние одной из них на другую (направленность и интенсивность). Связь между явлениями обязательно должна быть линейной, для четкого выяснения данного вопроса часто используют «геометрические представления», линейные схемы. (подробно на этом останавливаться не буду). Индекс корреляционной зависимости свидетельствует о интенсивности корреляции. (0,4 > г > 0,3 — слабая корреляция; 0,6 > г > 0,4 — средняя корреляция; г > 0,7 — сильная корреляция). Коэффициент корреляции (например коофициент Пирсона – как один из видов корреляционного анализа) можно легко подсчитать с помощью компьютерных программ (SPSS, Statistica, NCSS, Excel)

Перейдем к рассмотрению более сложного статистического анализа данных – факторного анализа. В его основе лежит процедура объединения Групп коррелирующих переменных («корреляционных узлов») в несколько факторов. (Объединяет группы переменных с группами переменных) Иными словами, цель факторного анализа — сконцентрировать исходную разнородную информацию в «общую картину» структурировано, логично, объединить факторы, иногда обладающие латентной, а не очевидной связью.

Рассмотрев цели, сущность двух видов анализа, делаем вывод, что корреляционный анализ призван просто находить взаимозависимость, объяснять ее интенсивность и трансформацию, а факторный анализ имеет более глобалную цель – структурое интегрирование информации в болки(факторы). Корреляционный анализ можно рассматривать как составную часть факторного анализа, (как и самостоятельный вид анализа) но это не умаляет достоинства первого т.к он выявляет определяющие связи. Факторный анализ более многоуровневый и сложный, позволяет сделать более глубокие выводы.

На мой взгляд, использование в политологии научного инструментария, заимствованного из других дисциплин может быть весьма полезно. Что касается статистческих методов, то они позволяют сделать исследование более релевантным, насыщенным и придают научную строгость. Однако, следует отметить, что не все явления в сфере политики можно измерить количественными методами. Не всегда можно перевести политическое событие в язык формул, цифр. Для каждого политического исследования необходимо выбирать методы изучения, исходя из особенностей изучаемого явления.

Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений.
     В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д.
     Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
     Пример. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.
     При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.
     Пример. Измерение курса акции некоторого предприятия. Возможные события заключаются в том, что стоимость акции Y примет некоторое значение в пределах от 0 до ∞.
     Пример. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.
     Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.
     Различают дискретные и непрерывные случайные величины.
     Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4).
     Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.
     Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.
     Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.
     Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
     Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:
    

     Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х1, х2, …, хn. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, … , n) образуют полную группу попарно независимых событий. Следовательно, р1  + р2 + …  + рn  = 1.
     Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения.