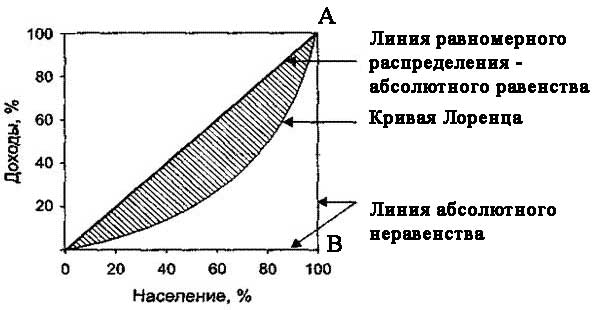
Кривая Лоренца – принцип построение и получения исходных данных.

Кривая Лоренца – это графическое изображение неравенства распределения доходов среди населения. Предложена в 1905 г. американским экономистом и статистиком Максом Отто Лоренцом (1876—1959). Кривая описывает, какую часть совокупного дохода общества получает каждая доля низкодоходных и высокодоходных домохозяйств.

Рассмотрим механизм построения кривой Лоренца. По оси Х откладывается доля населения (20%, 40% и т.д.), а по оси Y – доля доходов в обществе. Линию, отложенную под углом 45 градусов (линия ОА), можно считать линией равномерного распределения или абсолютного равенства. Естественно, ведь первых 20% (наибеднейших) населения владеют соответствующими 20% богатств, 40% населения – 40% богатств и т.д. Реальное же распределение будет всегда отличаться от этой прямой.

Распределение доходов по линиям ОВ-ВА соответствует абсолютному неравенству, так как все 100% доходов принадлежат всего одному домохозяйству, остальные же не имеют ничего.

На рисунке мы видим кривую Лоренца, которая интерпретируется достаточно просто: 20% наибеднейших домохозяйств обладают 5% совокупного дохода; 40% беднейших домохозяйств обладают 15% доходов и т.д. Чем более выпуклой является кривая, тем большим будет неравенство при распределении доходов в обществе.

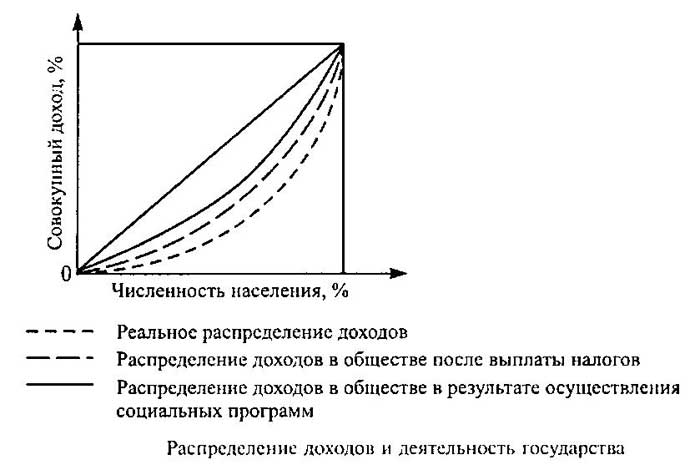
Кривые Лоренца наглядно демонстрируют политику выравнивания доходов, проводимую государством посредством налогообложения и разного рода социальных программ. При прогрессивной налоговой системе с более высоких доходов взимается более высокий налог. В результате различных социальных программ увеличиваются доходы наименее обеспеченной части населения. На основе соответствующих данных можно построить кривые Лоренца, которые отражали бы распределение доходов до выплаты налогов, после их уплаты и после получения выплат и пособий по социальным программам (см. рисунок).

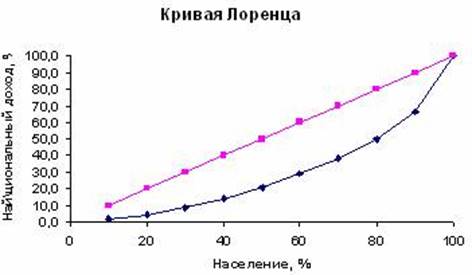
Чтобы построить кривую Лоренца, откладываем по оси X процент семей, а по оси Y - процент дохода Абсолютное равенство графически представлено биссектрисой ОЕ.

Линия фактического неравенства строится на основании данных о процентах дохода, приходящихся на каждые 10% населения. Если нижняя первая часть населения получила 3,2% всех доходов, то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 10% населения с процентами доходов вторых 10% населения (1,9% + 2,5%) и т.д.

Рассчитаем коэффициенты концентрации доходов (индекс Джини). 
Уровень неравенства определяется с помощью коэффициента Джини. Он рассчитывается как отношение площади фигуры OABCDKLMNPE к площади треугольника ОEG. Для того чтобы определить площадь фигуры, лежащей ниже кривой Лоренца, соединяем прямыми линиями точки ОА, АВ и т.д. Опускаем перпендикуляр на ось X и находим площади фигур, лежащих ниже точек А, B, С.

SABB'A состоит из треугольника и прямоугольника SBCCB' также состоит из треугольника и прямоугольника

Сложив все площади фигур, получим площадь фигуры S2

Площадь треугольника OEG находим по формуле:

Отсюда индекс Джини равен:

Определим децильный коэффициент дифференциации доходов.