Нелинейная регрессия— частный случай регрессионного анализа, в котором рассматриваемая регрессионная модель есть функция, зависящая от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной.
Модели, нелинейные по параметрам. Для сравнения с предыдущим примером рассмотрим зависимость между возрастом человека (переменная x) и его скоростью роста (переменная y). Очевидно, что соотношение между этими двумя переменными на первом году человеческой жизни (когда происходит наибольший рост) сильно отличается от соотношения во взрослом возрасте (когда человек почти не растет). Поэтому, эту зависимость лучше представить в виде какой-нибудь экспоненциальной функции с отрицательным показателем степени:
Рост = exp(-b1*Возраст)
Если вы построите на графике оценку для коэффициента регрессии, то вы получите кривую следующего вида:
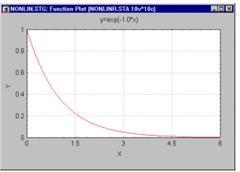
Отметим, что эта модель по своей природе больше не является линейной, т.е. выражение, написанное сверху, не представимо в виде простой регрессионной модели с некоторыми преобразованиями независимых переменных. Такие модели называются нелинейными по параметрам.
Сведение нелинейных моделей к линейным. В общем случае, всегда, когда регрессионная модель может быть сведена к линейной модели, этому способу отдается предпочтение (при оценивании соответствующей модели). Модель линейной множественной регрессии (см. Множественная регрессия) наиболее просто понимаема с точки зрения математики и, с практической точки зрения, наиболее проста для толкования. Поэтому, возвращаясь к простой экспоненциальной регрессионной модели Скорости роста как функции Возраста, описанной раньше, мы можем преобразовать это нелинейное уравнение в линейное, прологарифмировав обе части уравнения, получив:
log(Рост) = -b1*Возраст
Если теперь заменить log(Рост)) на y, мы получим стандартную модель линейной регрессии, как уже было показано раньше (без свободного члена, который был опущен для простоты изложения). Таким образом, для оценивания взаимоотношения возраста и скорости роста вы можете прологарифмировать данные о скорости роста (например, воспользовавшись преобразованиями таблиц данных с помощью формул), а затем использовать Множественную регрессию, получив при этом интересующий нас коэффициент регрессии b1.
Адекватность модели. Конечно, используя “неправильное” преобразование, можно прийти к неадекватной модели. Поэтому, после ”линеаризации” модели, наподобие только что показанной, очень важно провести подробное изучение статистик остатков, вычисляемых с помощью Множественной регрессии.
Поможем написать любую работу на аналогичную тему

