Задача 1. - КОНТРОЛЬНАЯ РАБОТА по дисциплине: «Эконометрика»

По предприятиям легкой промышленности региона получена информация характеризующая зависимость объема выпуска продукции (Y, млн.руб.)от объема капиталовложений (Х, млн.руб.).

Требуется:

1. Для характеристики Y от Х построить следующие модели:

- линейную,

- степенную,

- показательную,

- гиперболическую.

2. Оценить каждую модель, определив:

         - индекс корреляции,

         - среднюю относительную ошибку,

         - коэффициент детерминации,

         - F-критерий Фишера.

3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

4. рассчитать прогнозные значения результативного признака, если прогнозное значение фактора увеличится на 110% относительно среднего уровня.

5. Результаты расчетов отобразить на графике.

Задание к задаче№1

Таблица 1

Решение:

1.     Построение линейной модели парной корреляции.

           Определим  линейный коэффициент  парной корреляции по следующей формуле:

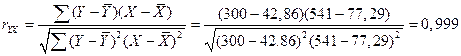
          По данным вычислениям видно, что связь между объемом капиталовложений и выпуском продукции прямая и достаточно сильная.

         Уравнение линейной регрессии имеет вид: 

Уравнение линейной регрессии имеет вид:

С увеличением  объема капиталовложений  на 1 млн. руб. объем выпускаемой продукции увеличивается в среднем на 558 тыс.руб. Это свидетельствует об прямой связи данных показателей и эффективности работы предприятия.

Расчеты производились исходя из данных, указанных в таблице 2,3

Таблица 2

Таблица 3

 Рассчитаем коэффициент детерминации:

           Вариация результата Y (объема выпуска продукции) на 99,8% объясняется вариацией фактора Х (объем капиталовложений).

Оценку значимости  равнения регрессии проведем с помощь. F-критерия Фишера:

 для ; , .

         Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. .

        Определим среднюю относительную ошибку:

Данный показатель отражает на сколько в среднем  расчетные значения  для линейной модели отличаются от фактических значений (на 3,455%).

2.     Построение степенной модели парной регрессии.

          Уравнение степенной модели имеет вид:   .

          Для построения этой модели необходимо произвести  линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

. 

Таблица 4

Обозначим Y=lg, Х=lgx, А=lga.

          Тогда уравнение имеет вид: Y=A+bX – линейное уравнение регрессии.

Рассчитаем его параметры, используя таблицу 5.

                                                                                       Таблица 5

         Уравнение регрессии будет иметь вид: .

        Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения и получим уравнение степенной модели регрессии.

.

Определим индекс корреляции:

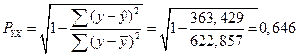
        Связь между показателем и фактором можно считать средней по силе.

Рассчитаем коэффициент детерминации:

Вариация результата Y (объема выпуска продукции) на 41,7% объясняется вариацией фактора Х.

Рассчитаем F-критерий Фишера:

 для ; , .

Средняя относительная ошибка:

         В среднем расчетные значения  для степенной модели отличаются от фактических значений на 0,287%.

3.     Построение показательной функции.

         Уравнение показательной кривой: .

         Для построения этой модели необходимо произвести  линеаризацию переменных. Для этого  произведем логарифмирование обеих частей уравнения:

, обозначим: , , .

Получим линейное уравнение регрессии: .

Рассчитаем его параметры, используя данные таблицы 6.

Таблица 6

Уравнение будет иметь вид: .

         Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:

Определим индекс корреляции:

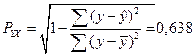
           Данный показатель характеризует среднюю связь между показателем и фактором.

Индекс детерминации: 

Вариация результата Y на 40,7% объясняется вариацией фактора Х.

Рассчитаем F-критерий Фишера:

 для ; , .

Средняя относительная ошибка:

В среднем расчетные значения  для степенной модели отличаются от фактических значений на 0,231%.

4.     Построение  гиперболической функции.

Уравнение гиперболической функции: .

Произведем линеаризацию модели путем замены Х=1/х.

В результате получим линейное уравнение: .

Рассчитаем его параметры по данным таблицы 7.

Таблица 7

           Получим следующие уравнение гиперболической модели: .

          Определим индекс корреляции:

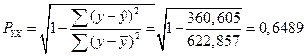
          Исходя их данного показателя силу связи можно оценить средним уровнем.

Индекс детерминации:

=0,421

          То есть вариация  результата Y (объема выпуска продукции) на 42,1% объясняется вариацией фактора Х (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

 для ; , .

Средняя относительная ошибка:

             В среднем расчетные значения у для гиперболической модели отличаются  от фактических значений на 0,0082%.

Для выбора лучшей модели построим сводную таблицу результатов:

Таблица 8

               В качестве лучшей модели для построения прогноза  можно взять линейную модель, так как она имеет большее значение F-критерия Фишера и коэффициента детерминации.

Расчет прогнозного значения результативного показателя:

             Прогнозное значение результативного признака (объема выпуска продукции) определим по уравнению линейной модели, подставив в него планируемую (заданную по условию) величину объема капиталовложений.

             По условию  нужно рассчитать прогнозное значение результативного признака (объема выпускаемой продукции), если  прогнозное значение фактора  увеличится на 110% относительно среднего уровня. Средний уровень  значения фактора (объема капиталовложений-Х) составляет 77,29млн. руб.

            При увеличении на 110% он составит 85,019 млн.руб.:

            Из этого уравнения следует, что при увеличении объема капиталовложений на 110% относительно среднего уровня объем выпуска продукции повысится в среднем до 47,708 млн.руб.

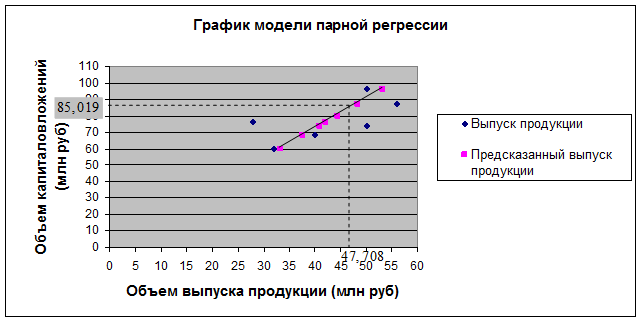
           Фактический, расчетные и прогнозные значения по лучшей модели отобразим на графике: