Задача 2.   - КОНТРОЛЬНАЯ РАБОТА по дисциплине: «Эконометрика»

       По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки по кредитам (), ставки по депозитам () и размера внутрибанковских расходов ().

Требуется:

1.     Осуществить отбор факторных признаков для построения двухфакторной регрессионной модели.

2.     Рассчитать параметры модели.

3.     Для характеристики модели определить:

-       линейный коэффициент множественной корреляции,

-       коэффициент детерминации,

-       средние коэффициенты эластичности,

-       бета-, дельта – коэффициенты.

Дать их интерпретацию.

4.     Осуществить оценку надежности уравнения регрессии.

5.     Оценить с помощь t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.

6.     Построить точечный и интервальный  прогнозы результирующего показателя.

7.     Отразить результаты расчетов на графике.

Задание к задаче 2.

Таблица 1

1.      Выбор факторных признаков для построения двухфакторной модели регрессии.

n=10, m=3

С помощью MS Excel проведем корреляционный анализ. Результаты корреляционного анализа представлены в таблице 2.

Таблица 2

Анализ матрицы коэффициентов парной корреляции показывает что Y имеет тесную связь со всеми факторами  но между факторами Х1 и Х3 связь теснее а значит можно говорить о мультиколлинеарности этих факторов поэтому мы выбираем фактор Х2

1.                 Выбор вида модели и оценка ее параметров.

С помощью MS Excel проведем регрессионный анализ, результаты отразим в таблицах 3, 4, 5, 6.

                                                           Таблица 3

                                  Таблица 4

                                                                                             Таблица 5

                                      Таблица 6

Уравнение регрессии зависимости объема прибыли от Ставки по кредитам и Ставки по депозитам можно записать в следующем виде:

у=33,295+0,767х1+0,017х2

2.      Оценка качества модели.

В таблице 14 приведены вычисленные по модели значения Y и значения остаточной компоненты.

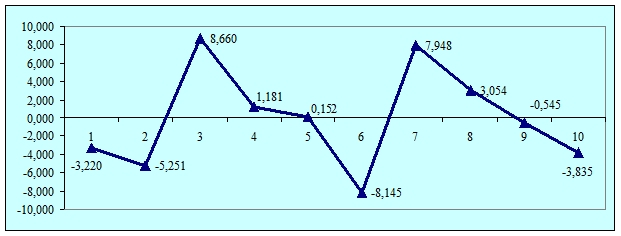
Рис.2

Вычислим для модели коэффициент детерминации.

Этот коэффициент уже вычислен нами и находится в таблице 3.

R2 = 0,855

Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:

Fтабл мы вычисляем с помощью функции FРАСПОБР

Fтабл = 4,737

Fрасч уже вычислено и находится в таблице 4

Fрасч = 20,621

Поскольку .Ррасч > Ртабл, уравнение регрессии следует признать адекватным.

Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициент эластичности (Э) и бета-коэффициент, которые соответственно рассчитываются по формулам:

Эj = аj*xср j / yср

b = ai * Sxi / Sy

Таблица 7

Э1 = 0,767*42,4/68,6 = 0,474

Э2 = 0,017*160,8/68,6 = 0,040

b = 0,767 * 304,7111 / 205,3778 = 1,138

b = 0,017 * 123,7333 / 205,3778 = 0,010

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент.

Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

2.                 Оценка статистической значимости

Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии а,, а2 приведены в четвертом столбце таблицы 5.

Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЫОДРАСПОБР

tтабл=  2,36462256

tрасч=0,704 

tрасч =4,604 критерий статистически значим

tрасч =0,066

3.                 Точечный и интервальный прогноз

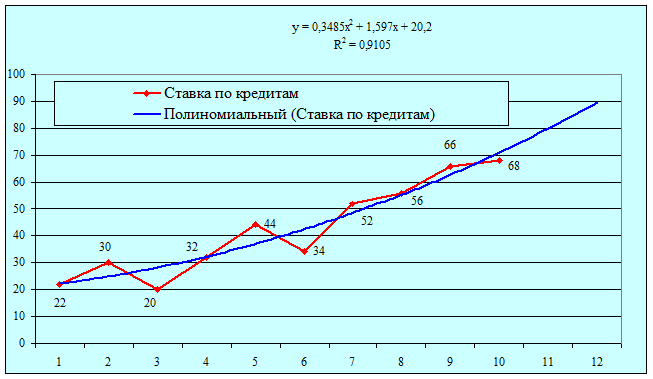Прогноз показателя «Ставка по кредитам»

Рис.1

Прогноз показателя «Ставка по депозитам»

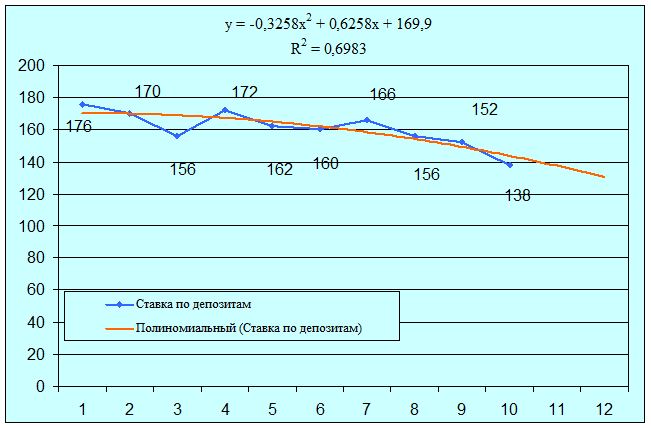Рис.2