1.Постройте корреляционное поле и по его виду визуально определите формулу зависимости между х и у.
2.Оцените выборочный коэффициент корреляции rxy. Проинтерпретируйте результат.
3.Оцените по МНК параметры уравнения линейной регрессии.
4.Проверьте статистическую значимость получения коэффициентов при уровне значимости a=0,05.
5.Оцените надежность полученного уравнения регрессии по критерии Фишера, для уровня значимости a=0,05.
6.Найти доверительные интервалы для коэффициента b1 и b0 найденной регрессии.
7. Сделать вывод по качеству построенной модели.
Решение
1.Имеется информация относительно среднего дохода (х) и среднего потребления (у). Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 1.
таблица 1.
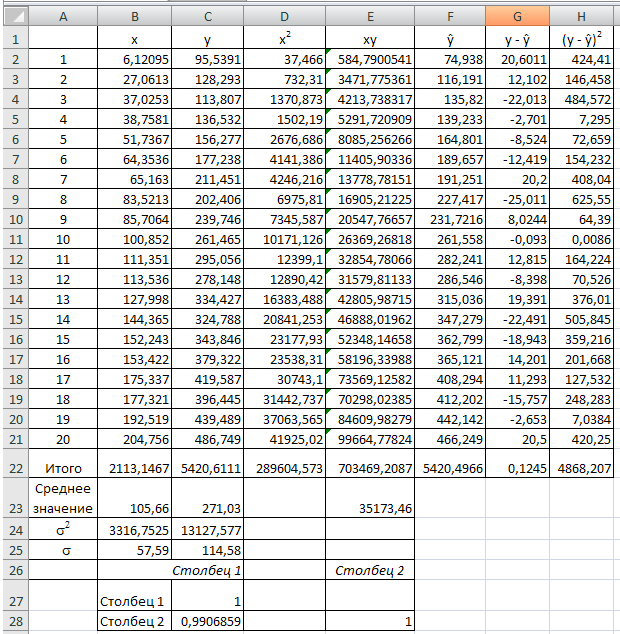
Для определения зависимости построим корреляционное поле. Проведем анализ регрессии.
рисунок 1.
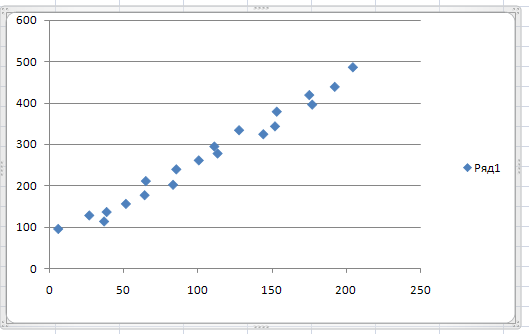
На рисунке 1 данные показаны в виде диаграммы рассеяния. Имеем положительную связь между средним доходом и средний потреблением.
По расположению точек полагаем, что связь между х и у линейная: ŷ=b0+b1x
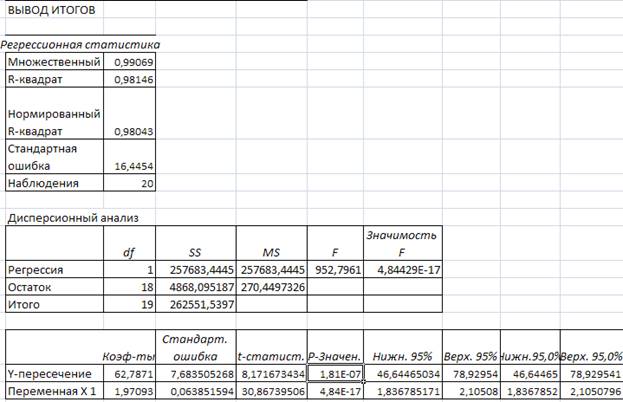
рисунок 2.
2. Для анализа силы линейной зависимости вычислим коэффициент корреляции rxy.
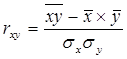
rxy=
=0.991
Данное значение коэффициента корреляции позволяет сделать вывод о достаточно тесной связи между рассматриваемыми переменными. Коэффициент детерминации rxy= 0.991; rxy2=0.982 указывает на то, что 98,2%- это доля вариации у объясненная вариацией фактора х , включенного в уравнение, а остальные 1,8 % вариации приходиться на долю других факторов, не учтенных в уравнении.
3. По МНК получим следующие уравнения линейной регрессии.
b0=
– b1
=271.03- 1.97*105.66=62.88
b1=
=
=1.97
4. Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначительном их отличии от нуля. Оценка значимости коэффициентов проводится путем сопоставления их значений с величиной случайной ошибки.
ta=
; tb= 
; tr= 
;
Случайные ошибки параметров определяются по формулам:
Sост= 
=
=16.44
mb0=Sост*
= 16.44*
= 7.68
mb1= 
= 
= 0.064
mr= 
= 
=0.032
Тогда:
ta= 
= 8.1875
tb= 
=30.78
tr= 
=30.97
Табличное значение при n=18, и a=0,05 составит tтабл.=2,1. Фактическое значение t- статистики превосходит табличное значение:
ta=8.1875>ttab=2.1;
tb= 30.78>ttab=2.1;
tr=30.97> ttab=2.1;
Гипотеза Н0 отклоняется, т.е. параметры b0, b1, rxy статистически значимы.
5. F –тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого применяется сравнение фактического и табличного Fтабл значения F-критерия Фишера.
Если Fтабл< Fфакт, то Н0 отклоняется.
Рассчитаем Fфакт через коэффициент детерминации rxy2:
Fфакт= 
* (n-2)= 
*18=981.9
Табличное значение при a=0,05 составляет Fтабл= 4,38 , т.к. Fфакт=981,9> Fтабл= 4,38, то уравнение регрессии признается статистически значимым.
6. Находим доверительные интервалы для коэффициентов.
Db0=t tab* mb0=2.1*7.64=16.044
Db1=ttab*mb1=2.1*0.064=0.1344
Формулы для расчета доверительных интервалов имеют следующий вид:
gb0= b0± Db0=62.88±16.044
gb0 min= b0-Db0=62.88-16.044=46.836
gb0max= b0+Db0=62.88+16.044=78.924
gb1=b1± Db1 =1.97±0.1344
gb1min=b1-Db1=1.97-0.1344=1.8356
gb1max =b1+Db1=1.97+0.1344=2.1044
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью Р=1-a= 0,95, параметры b0 и b1 не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.
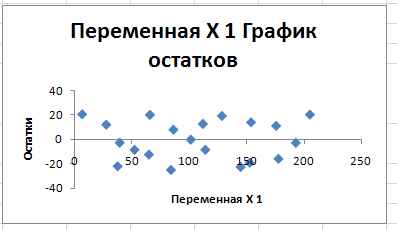
7. По всем статистическим показателям модель признается удовлетворительной. У нее высокие t- статистики, близкий к 1 коэффициент детерминации rxy2 . Отсутствует автокорреляция остатков. На основании этого считаем построенную модель качественной.
Поможем написать любую работу на аналогичную тему