1. Преобразовать исходные данные, чтобы модифицированная регрессии была линейной.
2.МНК получить оценки параметров a* и b*.
3.По оценкам a* и b* вычислить искомые оценки параметров a и b исходной регрессии.
Решение.
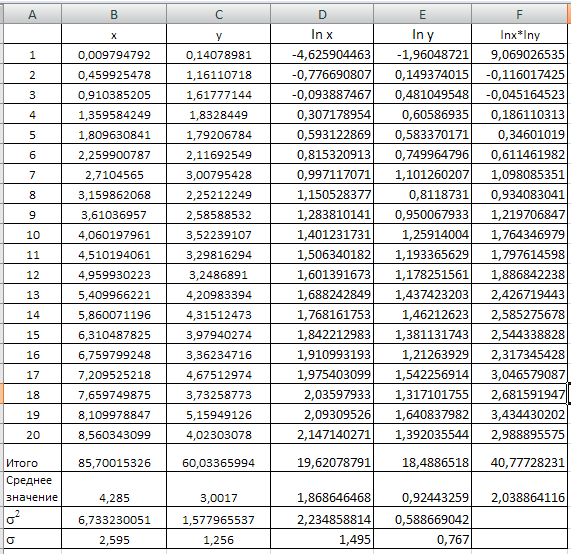
1. Задана нелинейная спецификация модели y=bxa * eE. Составим таблицу 1, рабочие расчеты по степенной функции регрессии.
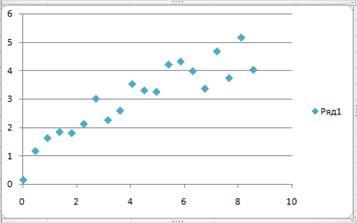
Построим диаграмму,
рис.1. Зависимость y=bxa * eE
2. Преобразуем начальную степенную функцию в линейный вид: y*=a*x*+b*.
Преобразуем данные модели: x*= lnx; y*=lny; a=a*;b= eb*, и занесем в таблицу.
3. Построим диаграмму, содержащую облако рассеяния преобразованных данных. Добавим линию тренда.
рис.2. Зависимость y*=a*x*+b*; a=a*;b= eb*
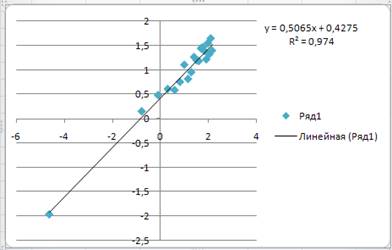
рис.3.
4. Находим оценки модифицированной линии регрессии a* и b*
b*=0,139
a*=0,665
5. Вычислим оценки параметров a и b исходной регрессии. Т.к. a=a*;b= eb*, тогда a=0,665, b=0,8485.
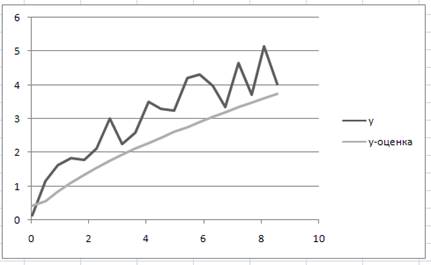
6.Формируем массив данных по исходной регрессии с вычисленными параметрами a и b. Оцененная регрессия вычисляется по формуле g=0,8485х0,665. Добавляем в диаграмму сформированный массив.
таблица 2
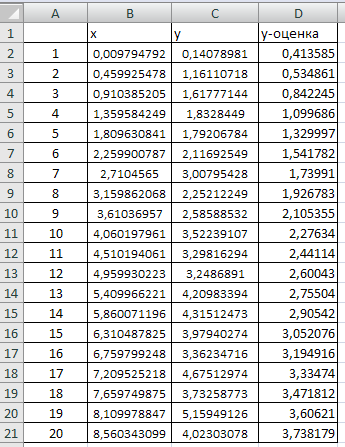
рис.4.
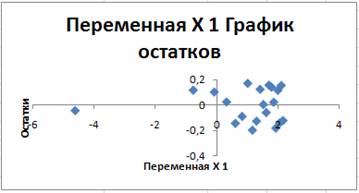
7. Сформируем ряд остатков от исходной регрессии. Вычислим статистику Дарбина- Уотсона.
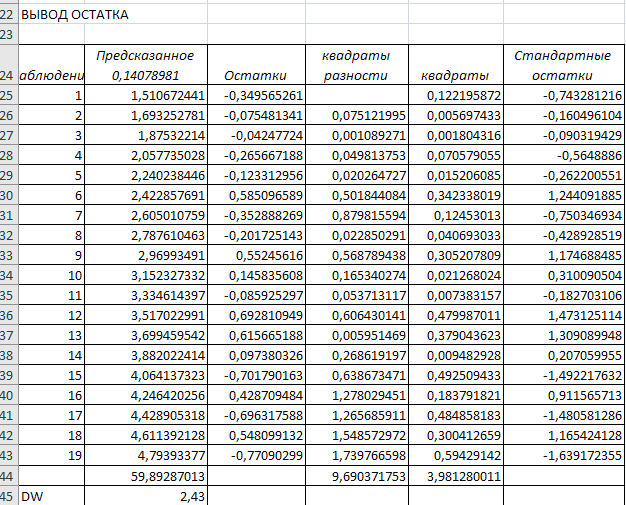
рис.5.
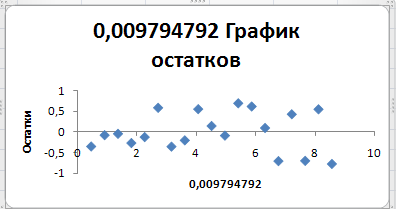
Т.к. DW»2, значит зависимость у от х линейная.
Поможем написать любую работу на аналогичную тему

