Даны значения ряда х(1), х(2)…х(n). Необходимо определить, имеет ли этот ряд неслучайную компоненту, зависящую от времени- тренд. Необходимо использовать критерий, основанный на выборочной медиане. Если установлено, что временной ряд имеет тренд, необходимо выделить этот тренд, т.е. сгладить временной ряд.
Решение.
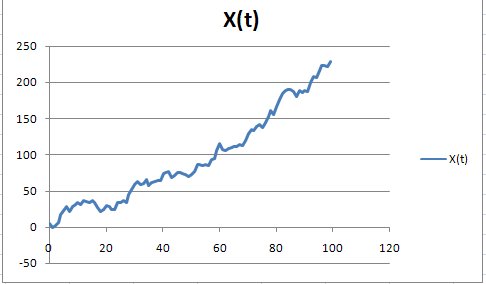
1.Строим диаграмму данного временного ряда.
|
t |
X(t) |
|
0 |
4,399 |
|
1 |
-1,005 |
|
2 |
1,102 |
|
3 |
6,075 |
|
4 |
16,45 Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
5 |
22,257 |
|
6 |
27,818 |
|
7 |
21,628 |
|
8 |
27,939 |
|
9 |
30,547 |
|
10 |
32,985 |
|
11 |
30,331 |
|
12 |
35,88 |
|
13 |
35,128 |
|
14 |
33,563 |
|
15 |
36,209 |
|
16 |
34,146 |
|
17 |
27,399 |
|
18 |
20,888 |
|
19 |
24,366 |
|
20 |
29,7 |
|
21 |
27,847 |
|
22 |
23,861 |
|
23 |
23,506 |
|
24 |
33,103 |
|
25 |
33,349 |
|
26 |
36,831 |
|
27 |
32,982 |
|
28 |
44,111 |
|
29 |
51,874 |
|
30 |
58,996 |
|
31 |
63,344 |
|
32 |
59,018 |
|
33 |
59,955 |
|
34 |
65,019 |
|
35 |
57,702 |
|
36 |
61,443 |
|
37 |
62,13 |
|
38 |
63,974 |
|
39 |
64,683 |
|
40 |
73,792 |
|
41 |
74,59 |
|
42 |
77,175 |
|
43 |
68,984 |
|
44 |
71,629 |
|
45 |
75,364 |
|
46 |
75,104 |
|
47 |
73,409 |
|
48 |
72,907 |
|
49 |
70,134 |
|
50 |
72 |
|
51 |
75,991 |
|
52 |
86,502 |
|
53 |
86,21 |
|
54 |
85,494 |
|
55 |
86,182 |
|
56 |
84,497 |
|
57 |
93,601 |
|
58 |
95,336 |
|
59 |
106,084 |
|
60 |
115,509 |
|
61 |
107,645 |
|
62 |
105,579 |
|
63 |
108,777 |
|
64 |
109,271 |
|
65 |
111,591 |
|
66 |
111,068 |
|
67 |
114,277 |
|
68 |
112,391 |
|
69 |
119,339 |
|
70 |
129,091 |
|
71 |
134,952 |
|
72 |
133,047 |
|
73 |
138,851 |
|
74 |
142,395 |
|
75 |
137,093 |
|
76 |
144,347 |
|
77 |
152,977 |
|
78 |
161,449 |
|
79 |
155,571 |
|
80 |
167,395 |
|
81 |
176,514 |
|
82 |
184,112 |
|
83 |
189,534 |
|
84 |
189,8 |
|
85 |
190,304 |
|
86 |
187,649 |
|
87 |
181,2 |
|
88 |
188,906 |
|
89 |
186,094 |
|
90 |
189,466 |
|
91 |
187,889 |
|
92 |
200,093 |
|
93 |
208,509 |
|
94 |
207,33 |
|
95 |
216,211 |
|
96 |
224,143 |
|
97 |
223,125 |
|
98 |
222,273 |
|
99 |
229,176 |
рис.1.
2.Находим выборочную корреляцию.
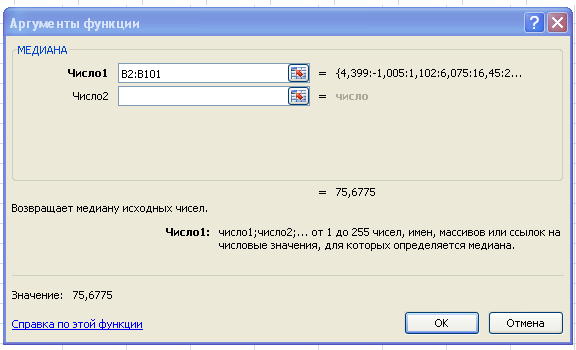
В нашем случае медиана равна 75,6775
3.Образуем ряд Z(1), Z(2),…Z(n)следующим образом Z(i)=ЗНАК(х(i)-хмед)
|
t |
X(t) |
Z(i) |
Серия |
|
0 |
4,399 |
-1 |
1 |
|
1 |
-1,005 |
-1 |
2 |
|
2 |
1,102 |
-1 |
3 |
|
3 |
6,075 |
-1 |
4 |
|
4 |
16,45 |
-1 |
5 |
|
5 |
22,257 |
-1 |
6 |
|
6 |
27,818 |
-1 |
7 |
|
7 |
21,628 |
-1 |
8 |
|
8 |
27,939 |
-1 |
9 |
|
9 |
30,547 |
-1 |
10 |
|
10 |
32,985 |
-1 |
11 |
|
11 |
30,331 |
-1 |
12 |
|
12 |
35,88 |
-1 |
13 |
|
13 |
35,128 |
-1 |
14 |
|
14 |
33,563 |
-1 |
15 |
|
15 |
36,209 |
-1 |
16 |
|
16 |
34,146 |
-1 |
17 |
|
17 |
27,399 |
-1 |
18 |
|
18 |
20,888 |
-1 |
19 |
|
19 |
24,366 |
-1 |
20 |
|
20 |
29,7 |
-1 |
21 |
|
21 |
27,847 |
-1 |
22 |
|
22 |
23,861 |
-1 |
23 |
|
23 |
23,506 |
-1 |
24 |
|
24 |
33,103 |
-1 |
25 |
|
25 |
33,349 |
-1 |
26 |
|
26 |
36,831 |
-1 |
27 |
|
27 |
32,982 |
-1 |
28 |
|
28 |
44,111 |
-1 |
29 |
|
29 |
51,874 |
-1 |
30 |
|
30 |
58,996 |
-1 |
31 |
|
31 |
63,344 |
-1 |
32 |
|
32 |
59,018 |
-1 |
33 |
|
33 |
59,955 |
-1 |
34 |
|
34 |
65,019 |
-1 |
35 |
|
35 |
57,702 |
-1 |
36 |
|
36 |
61,443 |
-1 |
37 |
|
37 |
62,13 |
-1 |
38 |
|
38 |
63,974 |
-1 |
39 |
|
39 |
64,683 |
-1 |
40 |
|
40 |
73,792 |
-1 |
41 |
|
41 |
74,59 |
-1 |
42 |
|
42 |
77,175 |
1 |
43 |
|
43 |
68,984 |
-1 |
44 |
|
44 |
71,629 |
-1 |
45 |
|
45 |
75,364 |
-1 |
46 |
|
46 |
75,104 |
-1 |
47 |
|
47 |
73,409 |
-1 |
48 |
|
48 |
72,907 |
-1 |
49 |
|
49 |
70,134 |
-1 |
50 |
|
50 |
72 |
-1 |
51 |
|
51 |
75,991 |
1 |
52 |
|
52 |
86,502 |
1 |
53 |
|
53 |
86,21 |
1 |
54 |
|
54 |
85,494 |
1 |
55 |
|
55 |
86,182 |
1 |
56 |
|
56 |
84,497 |
1 |
57 |
|
57 |
93,601 |
1 |
58 |
|
58 |
95,336 |
1 |
59 |
|
59 |
106,084 |
1 |
60 |
|
60 |
115,509 |
1 |
61 |
|
61 |
107,645 |
1 |
62 |
|
62 |
105,579 |
1 |
63 |
|
63 |
108,777 |
1 |
64 |
|
64 |
109,271 |
1 |
65 |
|
65 |
111,591 |
1 |
66 |
|
66 |
111,068 |
1 |
67 |
|
67 |
114,277 |
1 |
68 |
|
68 |
112,391 |
1 |
69 |
|
69 |
119,339 |
1 |
70 |
|
70 |
129,091 |
1 |
71 |
|
71 |
134,952 |
1 |
72 |
|
72 |
133,047 |
1 |
73 |
|
73 |
138,851 |
1 |
74 |
|
74 |
142,395 |
1 |
75 |
|
75 |
137,093 |
1 |
76 |
|
76 |
144,347 |
1 |
77 |
|
77 |
152,977 |
1 |
78 |
|
78 |
161,449 |
1 |
79 |
|
79 |
155,571 |
1 |
80 |
|
80 |
167,395 |
1 |
81 |
|
81 |
176,514 |
1 |
82 |
|
82 |
184,112 |
1 |
83 |
|
83 |
189,534 |
1 |
84 |
|
84 |
189,8 |
1 |
85 |
|
85 |
190,304 |
1 |
86 |
|
86 |
187,649 |
1 |
87 |
|
87 |
181,2 |
1 |
88 |
|
88 |
188,906 |
1 |
89 |
|
89 |
186,094 |
1 |
90 |
|
90 |
189,466 |
1 |
91 |
|
91 |
187,889 |
1 |
92 |
|
92 |
200,093 |
1 |
93 |
|
93 |
208,509 |
1 |
94 |
|
94 |
207,33 |
1 |
95 |
|
95 |
216,211 |
1 |
96 |
|
96 |
224,143 |
1 |
97 |
|
97 |
223,125 |
1 |
98 |
|
98 |
222,273 |
1 |
99 |
|
99 |
229,176 |
1 |
100 |
4.Сформируем серии. Серия-это группа подряд идущих +1 или -1
5.Применим критерий, основанный на выборочной медиане. Для этого найдем (n)- количество серий ; (n)- длина самой протяженной серии; v(n)=10; t(n)=76.
Рассчитаем теоретическое значение :
v(n)>0,5(n+2-1,96![]() =3.06
=3.06
t(n)<1.43 ln(n+1)=3.429
Т.к. неравенства не выполняются, тогда с вероятностью заключенной между 0,9025 и 0,95 делается вывод о наличии тренда.
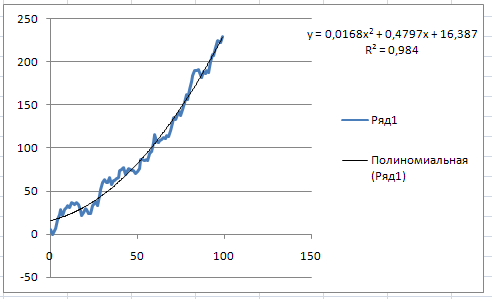
6. После того как установлено, что временной ряд имеет тренд, необходимо выделить этот тренд. Проверяем аналитическое сглаживание.
В результате получается:
рис.2.
7.Метод скользящего среднего.
Алгоритм скользящего среднего заключается в следующем:
ƒ(t)=![]()
t=m+1, m+2… n-m
При m=1 ƒ(1)=![]() х(1)+
х(1)+![]() и т.д.
и т.д.
При m=2 ƒ(2)=![]() и т.д.
и т.д.
При m=3 ƒ(3)= -![]() х(2)+
х(2)+![]() х(6)+(-
х(6)+(-![]() и т.д.
и т.д.
8.Метод экспоненциального взвешенного скользящего среднего (метод Брауна)
Метод скользящего среднего основывается на том, что все значения временного ряда имеют одинаковую информационную ценность. В задачах прогноза, в которых сглаженная функция (t) используется обычно для формирования прогнозов на несколько тактов вперед, недавние значения Х(t) очевидно ценнее, чем значение ряда в далеком прошлом, т.к. ряд далее будет вести себя тка, какова сформировавшаяся тенденция в настоящем и недалеком прошлом.
Получим сглаживание временного ряда по методу Брауна. λ возьмем равное 0,9
ƒ(t+1)= ![]() x (t+1)+ λ
x (t+1)+ λ ![]() * ƒ(t); t=1,2,3,,,
* ƒ(t); t=1,2,3,,,
ƒ(1)=x(1)
|
t |
X(t) |
m=1 |
m=2 |
m=3 |
|
0 |
4,399 |
|
|
|
|
1 |
-1,005 |
1,498667 |
|
|
|
2 |
1,102 |
2,057333 |
0,486486 |
|
|
3 |
6,075 |
7,875667 |
7,146943 |
7,007571 |
|
4 |
16,45 |
14,92733 |
15,22497 |
15,74552 |
|
5 |
22,257 |
22,175 |
23,6136 |
21,25876 |
|
6 |
27,818 |
23,901 |
24,75311 |
24,66471 |
|
7 |
21,628 |
25,795 |
25,09566 |
25,97524 |
|
8 |
27,939 |
26,70467 |
26,24726 |
27,8979 |
|
9 |
30,547 |
30,49033 |
31,27171 |
28,94543 |
|
10 |
32,985 |
31,28767 |
31,42354 |
32,10038 |
|
11 |
30,331 |
33,06533 |
32,71377 |
33,31086 |
|
12 |
35,88 |
33,77967 |
34,1664 |
33,81171 |
|
13 |
35,128 |
34,857 |
35,16777 |
34,66248 |
|
14 |
33,563 |
34,96667 |
34,7582 |
36,07529 |
|
15 |
36,209 |
34,63933 |
35,44229 |
34,94105 |
|
16 |
34,146 |
32,58467 |
33,72643 |
31,66833 |
|
17 |
27,399 |
27,47767 |
26,98474 |
27,48552 |
|
18 |
20,888 |
24,21767 |
22,42109 |
24,77295 |
|
19 |
24,366 |
24,98467 |
24,444 |
24,94352 |
|
20 |
29,7 |
27,30433 |
28,49169 |
26,36262 |
|
21 |
27,847 |
27,136 |
27,78614 |
26,28233 |
|
22 |
23,861 |
25,07133 |
23,81326 |
26,10114 |
|
23 |
23,506 |
26,82333 |
25,70234 |
26,51676 |
|
24 |
33,103 |
29,986 |
30,36957 |
30,15567 |
|
25 |
33,349 |
34,42767 |
35,33363 |
32,69367 |
|
26 |
36,831 |
34,38733 |
34,01306 |
35,08024 |
|
27 |
32,982 |
37,97467 |
36,46654 |
37,52367 |
|
28 |
44,111 |
42,989 |
42,30509 |
43,42895 |
|
29 |
51,874 |
51,66033 |
52,2904 |
51,38286 |
|
30 |
58,996 |
58,07133 |
59,31889 |
58,46633 |
|
31 |
63,344 |
60,45267 |
61,64369 |
60,41519 |
|
32 |
59,018 |
60,77233 |
60,30997 |
62,18157 |
|
33 |
59,955 |
61,33067 |
61,2726 |
61,24605 |
|
34 |
65,019 |
60,892 |
61,59497 |
60,5481 |
|
35 |
57,702 |
61,388 |
60,92066 |
61,09319 |
|
36 |
61,443 |
60,425 |
59,87246 |
61,276 |
|
37 |
62,13 |
62,51567 |
62,6874 |
60,8069 |
|
38 |
63,974 |
63,59567 |
62,96026 |
64,277 |
|
39 |
64,683 |
67,483 |
66,93266 |
67,25243 |
|
40 |
73,792 |
71,02167 |
71,49409 |
72,06671 |
|
41 |
74,59 |
75,18567 |
76,53237 |
74,17748 |
|
42 |
77,175 |
73,583 |
74,24571 |
74,18276 |
|
43 |
68,984 |
72,596 |
71,67183 |
72,75152 |
|
44 |
71,629 |
71,99233 |
71,22949 |
72,77762 |
|
45 |
75,364 |
74,03233 |
74,70871 |
73,09338 |
|
46 |
75,104 |
74,62567 |
75,09817 |
74,9399 |
|
47 |
73,409 |
73,80667 |
73,93117 |
73,865 |
|
48 |
72,907 |
72,15 |
72,0178 |
71,91471 |
|
49 |
70,134 |
71,68033 |
70,94177 |
70,73181 |
|
50 |
72 |
72,70833 |
71,4078 |
73,3209 |
|
51 |
75,991 |
78,16433 |
77,85254 |
77,86567 |
|
52 |
86,502 |
82,901 |
84,12754 |
82,78905 |
|
53 |
86,21 |
86,06867 |
86,94294 |
86,14148 |
|
54 |
85,494 |
85,962 |
85,97443 |
86,02967 |
|
55 |
86,182 |
85,391 |
84,73009 |
85,66557 |
|
56 |
84,497 |
88,09333 |
87,18157 |
87,05138 |
|
57 |
93,601 |
91,14467 |
90,64043 |
90,90462 |
|
58 |
95,336 |
98,34033 |
97,62611 |
98,9441 |
|
59 |
106,084 |
105,643 |
106,5666 |
106,2497 |
|
60 |
115,509 |
109,746 |
112,1616 |
108,9965 |
|
61 |
107,645 |
109,5777 |
109,6697 |
110,2577 |
|
62 |
105,579 |
107,3337 |
106,2162 |
108,4083 |
|
63 |
108,777 |
107,8757 |
107,7057 |
107,3854 |
|
64 |
109,271 |
109,8797 |
110,0595 |
109,2001 |
|
65 |
111,591 |
110,6433 |
110,6272 |
111,2568 |
|
66 |
111,068 |
112,312 |
112,3882 |
111,497 |
|
67 |
114,277 |
112,5787 |
112,3265 |
112,2266 |
|
68 |
112,391 |
115,3357 |
114,1018 |
115,0392 |
|
69 |
119,339 |
120,2737 |
119,396 |
121,1296 |
|
70 |
129,091 |
127,794 |
128,8493 |
126,64 |
|
71 |
134,952 |
132,3633 |
133,2934 |
132,4995 |
|
72 |
133,047 |
135,6167 |
135,2279 |
136,94 |
|
73 |
138,851 |
138,0977 |
138,561 |
137,8032 |
|
74 |
142,395 |
139,4463 |
139,996 |
138,512 |
|
75 |
137,093 |
141,2783 |
139,8857 |
141,2664 |
|
76 |
144,347 |
144,8057 |
143,5202 |
146,3589 |
|
77 |
152,977 |
152,9243 |
154,062 |
150,668 |
|
78 |
161,449 |
156,6657 |
157,4852 |
156,6401 |
|
79 |
155,571 |
161,4717 |
160,0675 |
161,6008 |
|
80 |
167,395 |
166,4933 |
165,5443 |
167,4255 |
|
81 |
176,514 |
176,007 |
176,6716 |
175,117 |
|
82 |
184,112 |
183,3867 |
184,3113 |
184,0432 |
|
83 |
189,534 |
187,8153 |
188,8162 |
188,5989 |
|
84 |
189,8 |
189,8793 |
190,5535 |
190,8325 |
|
85 |
190,304 |
189,251 |
190,0673 |
188,7137 |
|
86 |
187,649 |
186,3843 |
186,0561 |
187,0204 |
|
87 |
181,2 |
185,9183 |
184,8533 |
185,6377 |
|
88 |
188,906 |
185,4 |
185,3596 |
185,765 |
|
89 |
186,094 |
188,1553 |
188,4799 |
185,9368 |
|
90 |
189,466 |
187,8163 |
186,9063 |
188,4638 |
|
91 |
187,889 |
192,4827 |
191,0003 |
192,5673 |
|
92 |
200,093 |
198,8303 |
199,0848 |
198,3246 |
|
93 |
208,509 |
205,3107 |
206,3265 |
204,2468 |
|
94 |
207,33 |
210,6833 |
209,9583 |
211,9195 |
|
95 |
216,211 |
215,8947 |
215,9532 |
216,785 |
|
96 |
224,143 |
221,1597 |
222,6758 |
219,9265 |
|
97 |
223,125 |
223,1803 |
223,2559 |
|
|
98 |
222,273 |
224,858 |
|
|
|
99 |
229,176 |
|
|
|
Поможем написать любую работу на аналогичную тему

