Существует несколько методов: 1)метод наименьших квадратов: один из наиболее распространенных.Суть нужно рассчитать такие значения коэ-тов ß0иß1,к-ые миним. бы сумму квадратов отклонения наблюдаемых значений результативной переменной у от теоретических значений у⁻ b1=∑(x-x⁻)(y-y⁻)/∑(x-x⁻)2 b0=y¯-b1*x⁻2) Метод максимального правдоподобия, теоретически обоснованный математиком Р. Фишером. Идея метода заключается в том, что вся получаемая в результате многократных наблюдений информация об истинном значении измеряемой величины и рассеивании результатов сосредоточена в ряде наблюдений. Суть метода максимального правдоподобия заключается в нахождении оценок, при которых функция правдоподобия достигает наибольшего значения.3)Метод моментов нахождения оценок в математической статистике - это способ построения оценок, основанный на уравнивании теоретических и выборочных моментов. Пусть 
- выборка из распределения 
, зависящего от параметра 
. Пусть есть функция 
, такая что g(X1) интегрируема
относительно меры 
, и
,
где 
- биекция. Тогда оценка
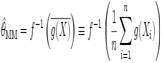
называется оценкой параметра 
методом моментов.
Поможем написать любую работу на аналогичную тему