Множественная регрессия. Требования, предъявляемые к факторам, включенным в модель.

При рассмотрении экономических процессов чаще всего приходится обращаться к моделям, содержащим более одного фактора-признака.

Таким образом, следует включить в модель не один фактор, а несколько, т.е. построить уравнение множественной регрессии.

Уравнение множественной регрессии имеет вид:

y=f(x1,x2,…,xk)

Простейшая функция для построения множественной регрессионной модели – линейная:

y = a + b1x1 + b2x2 +…+ bkxk +ε.

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике.

Основная цель – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное воздействие на моделируемый показатель.

Требования, предъявляемые к факторам, для включения в модель:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, когда Ryx1<Rx1x2 для зависимости y = a + b1x1 + b2x2 + ε может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

3. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R2, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других, не учтенных в модели факторов, оценивается как 1— R2 с соответствующей остаточной дисперсией S2.

При дополнительном включении в регрессию р+1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:

R2p+1  R2p  и  S2p+1  S2p.

Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор xp+1 не улучшает модель и практически является лишним фактором.

Отбор факторов обычно осуществляется в две стадии:

- отбираются факторы, исходя из сущности проблемы

- на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии.

Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если rxixj³0,7.

Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, т.е. Rxixj=0, то коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Основой измерения показателей тесноты связей является матрица парных коэффициентов корреляции

По этой матрице можно судить о тесноте связи факторов с результативным признаком и между собой. Хотя все эти показатели относятся к парным связям, все же матрицу можно использовать для предварительного отбора факторов для включения в уравнение регрессии. Не рекомендуется включать в уравнение факторы слабо связанные с результативными признаками, но тесно связанные с другими факторами.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов.

Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

- затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

- оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

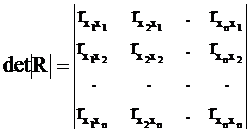
Чем det|R| ближе к нулю, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии.