Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например
– полиномы различных степеней – 
– равносторонняя гипербола –
–полулогарифмическая функция – 
.
2. Регрессии, нелинейные по оцениваемым параметрам, например
– степенная – 
;
– показательная – 
;
– экспоненциальная – 
.
- логистическая –
,
- обратная – 
.
Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:
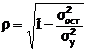, где 
– общая дисперсия результативного признака y,
– остаточная дисперсия.
Так как 
и 
, то индекс корреляции можно выразить как
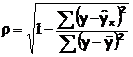
Величина данного показателя находится в пределах: 0£r£1. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Поможем написать любую работу на аналогичную тему