Построение двухмерной линейной модели корреляционно-регрессионного анализа.

Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров.

Линейная регрессия сводится к нахождению уравнения вида   или

Уравнение вида  позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее параметров а и b.

Оценки параметров линейной регрессии могут быть найдены разными методами. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) минимальна:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:

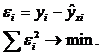
Решается система нормальных уравнений:

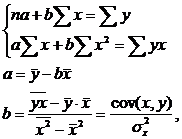
где  ,  и   - средние значения факторов Х, Y и их произведения;

         cov(x,y) – ковариация признаков.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.  Так, если в функции издержек  (у— издержки (тыс. руб.), x — количество единиц продукции), с увеличением объема продукции (x) на 1 ед. издержки производства возрастают в среднем на 2 тыс. руб., т. е. дополнительный прирост продукции на 1 ед. потребует увеличения затрат в среднем на 2 тыс. руб.

Формально а  — значение у при x = 0. Если признак-фактор x не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать параметр а  могут привести к абсурду, особенно при а < 0,

Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация результата меньше вариации фактора.

Уравнение регрессии всегда дополняется показателем тесноты связи.

При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэффициента корреляции.

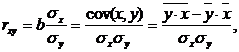
где  - среднее квадратическое отклонение факторного признака, которое определяется по формуле:

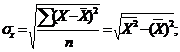
           - среднее квадратическое отклонение результативного признака, которое определяется по формуле:

Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии:

Область допустимых значений линейного коэффициента парной корреляции от -1 до +1. Знак коэффициента корреляции указывает направление связи. Если  , то связь прямая; если  , то связь обратная.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака Y, объясняемую регрессией (а, следовательно, и фактором Х), в общей вариации (дисперсии) Y. Коэффициент принимает значения от 0 до 1. Коэффициент детерминации – квадрат коэффициента или индекса корреляции.

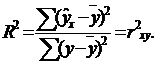
Соответственно величина  характеризует долю дисперсии Y, вызванную влиянием прочих неучтенных в модели факторов и ошибками спецификации.