Если измеряемая физическая величина У является функцией нескольких аргументов хi,
![]()
(7.1)
(например, косвенно определяемая величина либо результат измерения информационно-измерительной системы по результатам измерения нескольких каналов), то, представив У = Уи + D, хi = хиi + Di , где индекс "и" относится к истинному значению, D - соответствующая абсолютная погрешность, разложив функцию У в ряд Тейлора и пренебрегая членами выше первого, получаем приближенное выражение
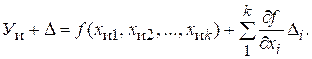
(7.2)
С учетом того, что первое слагаемое представляет собой выражение для истинного значения измеряемой величины, результирующая погрешность равна
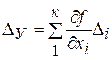
(7.3)
Для нахождения связи среднего квадратического отклонения результирующей случайной погрешности с числовыми характеристиками частных погрешностей можно обратиться к теореме о дисперсии линейной функции. При этом в общем случае будем считать, что случайные величины хi и хj зависимы, т.е. закон распределения одной из них может зависеть от значения, которое при данном опыте приняла другая величина. Среднее квадратическое отклонение результирующей случайной погрешности равно
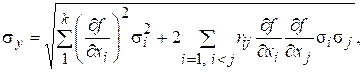
(7.4)
где sу, si, sj - средние квадратические погрешности величины У, i и j аргументов соответственно; rij - коэффициент корреляции между случайными погрешностями i и j аргументов. Обозначив
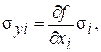
формулу (9.4) можно представить в виде
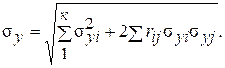
(7.5)
В частном случае при двух слагаемых погрешности
Если величины х1, х2, …, хk независимы, то коэффициент rij равен нулю при любых i и j. В этом случае формула (7.4) упрощается:
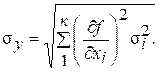
(7.6)
Таким образом, средняя квадратическая погрешность функции некоррелированных аргументов равна корню квадратному из суммы квадратов произведений частных производных функций по каждому из аргументов на средние квадратические погрешности соответствующих аргументов.
В случае, когда величина У связана с независимыми случайными аргументами хi соотношением
![]()
где А - постоянный множитель, относительная результирующая погрешность dу может быть найдена на основании (9.3) по следующей формуле:
![]()
(7.7)
где dхi - относительная погрешность отдельных аргументов.
Результирующее относительное среднее квадратическое отклонение sу = =s/у, выраженное через относительные средние квадратические отклонения аргументов s0i = si/xi, может быть найдено через соотношение, полученное на основании (9.5) при условии rij = 0:
![]()
(7.8)
Для случая n = m = …
Когда функция У определяется суммированием аргументов
![]()
результирующая погрешность Dу равна сумме абсолютных погрешностей составляющих аргументов:
![]()
(7.9)
Результирующее среднее квадратическое отклонение находится по формуле
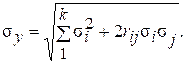
(7.10)
Так, для двух слагаемых
![]()
(7.11)
Для последнего случая при rij = 1
![]()
(7.12)
Поможем написать любую работу на аналогичную тему

