Результат косвенного измерения находят по данным прямых измерений нескольких величин (аргументов), связанных известной функциональной зависимостью с искомым результатом.
Вначале рассмотрим простейший случай, когда искомая величина 
определяется как сумма двух величин Х1 и Х2: 
.
Поскольку результаты прямых измерений величин Х1 и Х2 (после исключения систематических погрешностей) включают в себя некоторые случайные погрешности, то формулу косвенного измерения суммы можно переписать в виде 
,
Где 
- средние арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин 
и 
; 
- случайные погрешности величин и ; 
- оценка истинного значения косвенно измеряемой величины и ее случайная погрешность.
Вытекает справедливость двух последних равенств: 
; 
, т.е. оценкой истинного значения косвенно измеряемой величины должна служить сумма оценок истинных значений исходных величин, случайные погрешности которых складываются.
Математическое ожидание оценки 
равно сумме истинных значений величин X1 и X2 и, следовательно, является истинным значением измеряемой величины Y: 
ее дисперсия составляет
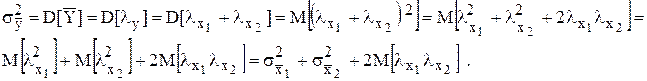
Математическое ожидание произведения случайных погрешностей называется корреляционным моментом и определяет степень «тесноты» линейной зависимости между погрешностями. Вместо корреляционного момента часто пользуются безразмерной величиной, называемой коэффициентом кор-реляции: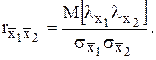 
Отсюда, в частности, следует, что коэффициент корреляции между погрешностями 
и 
средних арифметических равен коэффициенту корреляции между погрешностями результатов отдельных измерений величин X1 и X2: 
.
С учетом коэффициента корреляции с.к.о. результата косвенных измерений, т.е. оценки истинного значения косвенно измеряемой величины, будет 
.
Если погрешности измерения величин X1 и X2 некоррелированы, то: 
.
В тех случаях, когда теоретические с.к.о. результатов прямых измерений неизвестны, определяется оценка 
с.к.о. результата косвенных измерений через оценки с.к.о. 
и 
: 
.
Оценки коэффициента корреляции 
вычисляют на основании результатов прямых измерений исходных величин: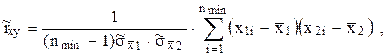 
где nmin - наименьшее из чисел наблюдений n1 и n2 .
При положительной корреляции, т.е. когда 
одна из погрешностей имеет тенденцию возрастать при увеличении другой, если же корреляция отрицательна, то 
и погрешность измерения одной величины обнаруживает тенденцию к уменьшению при увеличении погрешности измерения другой величины. Возможные значения коэффициента корреляции лежат в интервале 
. Если 
, то погрешности измерения некоррелированы.
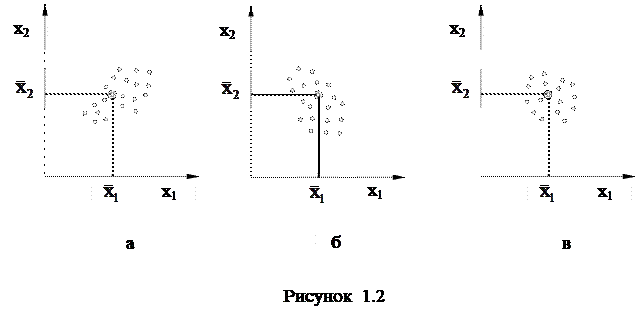
О наличии корреляции удобно судить по графику, на котором в координатах 
изображены пары последовательно получаемых результатов измерения величин X1 и X2 .
На рисунке 1.2 изображены случаи совместного распределения результатов измерения при положительной (рисунок 1.2,a) и отрицательной (рисунок 1.2,б) корреляции. Результаты измерений на рисунке 1.2,в некоррелированы.
Чаще всего наличия корреляции следует ожидать в тех случаях, когда обе величины измеряются одновременно однотипными средствами измерений, причем измерения внешних влияющих величин (электрических, магнитных, температурных, условий питания и прочее) одновременно заметно влияют на формирование случайных погрешностей их измерения. В некоторых случаях причиной корреляции между результатами измерений может стать сам проводящий измерения, т.к. искусство и опыт наблюдателя показывают значительное влияние на результаты измерений.
В тех же случаях, когда исходные величины измеряют с помощью различ-ных средств измерения в разное время, можно с полным правом ожидать, что результаты, если и будут коррелированы, то очень мало, и коэффициентом корреляции можно пренебречь.
При неизвестных с.к.о. слагаемых следует подставлять их оценки 
, а оценки коэффициентов корреляции вычисляют по формуле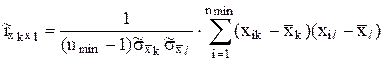 
,где nmin - наименьшее из чисел наблюдения Xk и Xl .
Если исходные измерения независимы, то все коэффициенты корреляции равны нулю и с.к.о. оценки Y определяют с помощью более простого выражения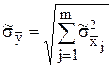 
.
Произведения частных производных уравнения косвенного измерения на с.к.о. результатов измерения соответствующих аргументов называются част-ными погрешностями косвенного измерения: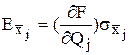 
.
Таким образом, в качестве наиболее достоверного значения 
косвенного измеряемой величины Y следует понимать значение, получаемое подстановкой в формулу (1.64) косвенного измерения средних арифметических 
рядов измерений искомых величин; с.к.о. этой оценки определяется из формулы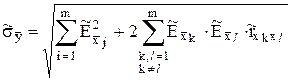 
, причем значения частных производных вычисляются при средних арифметических значениях аргументов 
.
Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений. В этих условиях для вычисления доверительного интервала случайной погрешности 
, рассчитываемого по формуле 
, используется значение коэффициента tp , прямо выбираемое из таблицы Ж.1 при количестве измерений n>30. Если же n£30 , предварительно должно быть определено “эффективное” число степеней свободы, которое затем учитывается при определении tp: 
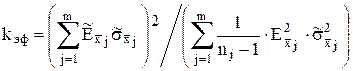,где nj
– число прямых измерений величины Xj :
Поможем написать любую работу на аналогичную тему