Пусть имеется выборка из n измеряемых величин х1, х2, ... хn. Результаты измерений содержат только случайные погрешности. Требуется найти оценку истинного значения измеряемой величины и погрешность измерения в данной выборке.
При симметричных законах распределения вероятностей истинное значение измеряемой величины совпадает с ее математическим ожиданием, а оценкой математического ожидания является среднее арифметическое результатов отдельных наблюдений:
.
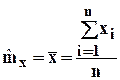Если известно математическое ожидание случайной величины, то СКО результатов наблюдений равно
.
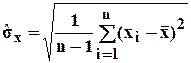Проверить результаты наблюдений на наличие грубой погрешности можно следующим образом:
Если |xi - 
| ³ 3, то данный результат содержит грубую погрешность и должен быть исключен.
Полученная выше оценка истинного значения измеряемой величины Х является случайной величиной, рассеянной относительно Q. СКО результата измерения будет иметь следующий вид:
.
Эта величина характеризует рассеяние среднего арифметического значения результатов n наблюдений измеряемой величины относительно ее истинного значения и является точечной оценкой.
На практике используются интервальные оценки, так называемые доверительные интервалы, которые связаны с СКО следующим соотношением:
, где
t – коэффициент, зависящий от вида распределения случайных величин, количества наблюдений и доверительной вероятности.
Поможем написать любую работу на аналогичную тему