Погрешности измерений и теория вероятности

Рассмотрим, как располагаются значения 5Г вокруг среднего значения. Для этого проведем серию замеров одной и той же величины и отобразим их результаты на таблице (Рис.2). Допустим, мы измеряем длину вала, номинальное (модельное) значение которой равно 100 мм. Возьмем листок бумаги «в клеточку» и в нижней его части проведем ось. Посередине поставим значение 100, а слева и справа последовательность значений с шагом 0,01 мм. Измерив значение величины, мы поставим крестик в клеточки над этим значением. Если результаты последующих измерений будут равняться тому же значению, крестик поставим клеточкой выше. Такой метод называется «Метод контрольных листков» и широко применяется на практике при анализе причин появления некачественной продукции.

Рис. 2. Контрольный листок

В нашем примере значение 99.99 встретилось 7 раз, 100,02 - 2 раза, а 100,05 ни разу.

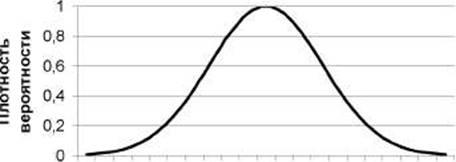
Проделав достаточно большое число замеров, мы получим «горку». Изучив, таким образом, множество измерений совершенно различных величин, мы заметим, что форма «горки» (Рис. 3) оказывается схожей для всех них. Впервые дал этому математическое объяснение немецкий математик Гаусс. Но прежде чем рассказывать о его исследованиях нам придется познакомиться с основными понятиями теории вероятности. Вы будете подробно изучать этот курс. Поэтому сейчас мы остановимся только на некоторых, нужных для понимания метрологии, понятиях и фактах.

10

Рис. 3. Теоретические кривые Гаусса для различных распределений.

Назовем случайной величиной процесс, численную характеристику, которого нельзя предсказать заранее. Очевидно, многократное измерение одной величины является примером такого процесса. Частотой (Nm) появления определенного значения (m) случайной величины назовем количество случаев, в которых случайная величина принимает данное значение. В нашем примере частота значения 99,99 равна 7. Если мы предполагаем, что частоты появления различных значений отражают свойства самой случайной величины, желательно выразить эти свойства вне зависимости от числа испытаний (в нашем примере, замеров). Назовем вероятностью того, что случайная величина примет данное значение, предел отношения:

Pm= Lim (Nm/N)

N-

(4)

Где Nm - частота появления значения m; N - общее число испытаний.

Равенство полученного значения случайной величины определенному значению это событие в нашем вероятностном мире. Если события не зависят друг от друга, то вероятность появления какого - либо из них равна сумме их вероятностей2 . Вероятность появления хоть какого-то события равна единице.

События, изображенные на рис. З находятся так близко друг от друга, что их можно представить в виде непрерывной последовательности. Тогда кривую, похожую на шляпу гнома, можно интерпретировать как плотность вероятности, показывающую, насколько изменится вероятность события, если величина изменится на единицу.

Вероятность
события X < X0
будет равна
площади под
кривой,            от

линии X = X0 до -со (Рис. 4) .

11

Рис 4. Оценка вероятности событий по графику функции плотности вероятности Вероятность события X< -5 равна заштрихованной площади в левой части рисунка, вероятность X > 5, 5 равна заштрихованной площади в правой части рисунка.

Вся площадь под кривой - вероятность того, что Х примет хоть какое то значение равна единице. Тогда, вероятность того, что Х находится в интервале: X1<X<X2 равна единице минус заштрихованная площадь слева и справа. Выбрав X1 и X2 такими, чтобы заштрихованная площадь была небольшой (например, 0,01), мы можем сказать: «С доверительной вероятностью 1- 0,01= 0,99 величина X находится в интервале (X1; X2).

Характеристики распределения случайной величины

Как видно из рис. З, различные случайные величины имеют различный разброс своих значений. Наглядно это показывает различная ширина «шляп». В теории вероятности рассматриваются несколько характеристик случайных величин:

Среднее значение - предел отношения суммы всех значений к общему числу наблюдений:

Xcp=Lim(ZXm)/N                                            (5)

Для оценки среднего значения используется допредельное выражение при достаточно большом числе испытаний

Xcp~l/N*IXm                                                                                      (6)

Если случайная величина может принимать только определенные значения: X1 X2 Xm и известны вероятности появления этих значений P1 P2 Pm, среднее значение может быть вычислено по формуле:

 Р1                                                                                       (7)

Дисперсия  - мера разброса значений  случайной  величины,  определяется  как среднее значение квадрата отклонения случайной величины от ее среднего значения:

D=Lim(Z(Xm-Xcp)2/N)                                      (8)

Для оценки дисперсии при достаточно большом числе испытаний используется формула:

D ~ 1/(N*(N-1))*Z (Xm - Хср)2                                                   (9)

Если  случайная  величина  может  принимать только  определенные значения  с известными вероятностями, дисперсия вычисляется по формуле:

12

D = 1/(M*(M-1))*I (Xi - Xср)2 * Pi Где M - число различных значений Х.

(10)

Величина D характеризует разброс значений вокруг среднего. В случае измерений, D может использоваться в качестве меры случайной погрешности измерения. Однако, применение D не удобно. Дело в том, что размерность D равна квадрату размерности измеряемой величины. Например, мы измеряем расстояние в метрах. Подставим в (10) результаты наших замеров. Размерность D получилась равной м2. Поэтому вместо D, в качестве меры случайной ошибки, применяют величину о - называемую среднеквадратическим отклонением.

о =Vd = V(i/(M*(M-i))*z (Xi -Xср)2 * ро         (11)

Для распределения Гаусса справедливо соотношение: «Вероятность, того, что значение величины отличается от среднего значения более чем на Зо меньше 0,01. Таким образом, мы можем использовать о как меру погрешности нашего измерения.

Отступление для программистов. Как бороться с грубыми ошибками?

При организации ввода данных в нашу информационную систему мы можем использовать вероятностный метод выявления грубых ошибок в данных. Как мы видели, отклонения значения величины за Зо маловероятны. Организуем ввод данных так, чтобы сразу считать Xср и о для уже введенных данных. Тогда, при появлении значения отличающегося от среднего больше чем на Зо, программа выдает сообщение: «Введенное значение маловероятно! Пожалуйста, проверьте правильность ввода». Вовсе не обязательно, что мы ошиблись. Но проверить стоит. Таким образом, компьютер обращает внимание оператора на маловероятную информацию, что позволяет сократить число грубых ошибок.

Что мы понимаем под погрешностью измерений

В таблице 3 сведены различные ситуации применения термина «погрешность измерения».

Таблица 3

13

Способы представления погрешности

В зависимости от решаемых задач используются несколько способов представления погрешности:

•      Абсолютная погрешность - измеряется в тех же единицах что и измеряемая
величина.    Характеризует    величину    возможного    отклонения    истинного    значения
измеряемой величины от измеренного.

•      Относительная погрешность - отношение абсолютной погрешности к значению
величины. Если мы хотим определить погрешность на всем интервале измерений, мы
должны    найти    максимальное   значение    отношения    на   интервале.    Измеряется    в
безразмерных единицах.

•      Класс точности - относительная погрешность, выраженная в процентах. Обычно
значения класса точности выбираются из ряда: 0,1; 0,5: 1,0; 1,5; 2,0; 2,5 ...