Обработка результатов измерений с многократными наблюдениями

Обработка результатов измерений с многократными наблюдениями

1. Проводится обнаружение, оценка и исключение систематических погрешностей из измеренных значений или результатов наблюдений (т.е. производится их исправление). Неисключенные систематические погрешности должны быть просуммированы между собой для получения доверительных границ неисключенной систематической погрешности Δс.

2.        Проверяется принадлежность исправленных измеренных значений или результатов к нормальному распределению или оно таковым принимается.

3.        При прямых измерениях по формуле (4.12) рассчитывается значение , а при косвенных измерениях – значения .

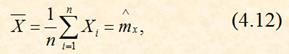
4.        По формуле (4.14) вычисляются случайные отклонения Vi и с помощью соотношения

проверяется правильность расчетов  и Vi.

5.      По формуле (4.15) вычисляются оценки выборочного стандартного отклонения

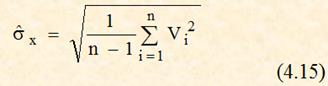
6.      С помощью критерия (4.18) или другого проверяется наличие грубых погрешностей. Измеренные значения показания, содержащие грубую погрешность, исключаются из ряда, и вычисления по пп. 3-5 повторяются.

7.      По формуле (4.16) вычисляются оценки выборочного стандартного отклонения среднего арифметического

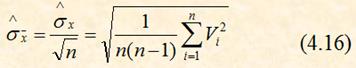
8.      . Для косвенных измерений по формуле (4.19) рассчитываются    и по формуле (4.20) оценка  .

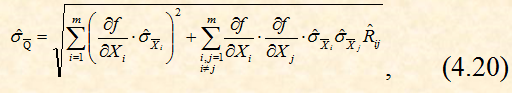
9.      По заданной доверительной вероятности Pд и числу наблюдений n определяется коэффициент Стьюдента t.

10.  По формуле (4.17) для прямых измерений или по формуле (4.25) для косвенных рассчитываются доверительные границы случайной погрешности результата измерения .

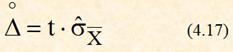
11.  Определяются доверительные границы суммарной погрешности результата измерения Δ. В случае прямых измерений вычисляют отношение  . Если оно меньше 0.8, то значением  пренебрегают по сравнению с  и принимают, что. Если отношение больше 8, то пренебрегают значением  и принимают  . Если же эти неравенства не выполняются , то Δ определяется по формуле

где К – коэффициент, зависящий от соотношения случайной и неисключённой систематической погрешности, определяемый по формуле

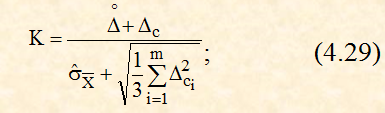
            SΣ  – оценка суммарного среднего квадратического отклонения результата измерения, определяемая по формуле

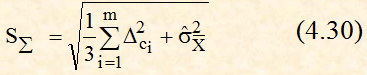
Таким образом, с учетом (4.29) и (4.30)

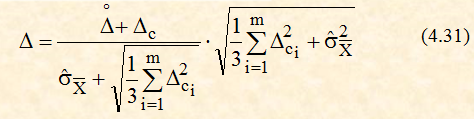
На практике пользуются упрощенной формулой вида:

12.   Записывается окончательный результат измерения по одной из стандартных форм.

_________________________________________________________