Эволюционный процесс математически описывается векторным полем в фазовом пространстве (абстрактном пространстве с числом измерений, равном числу переменных, характеризующих состояние системы). Точка фазового пространства задает состояние системы. Приложенный в этой точке вектор указывает скорость изменения состояния. В случае затухания фазовые траектории при любых начальных значениях оканчиваются в одной точке, которая соответствует покою. В таких точках вектор может обращаться в нуль. Такие точки называются положениями равновесия (состояние не меняется с течением времени). Фазовые траектории создают складки внутри фазового пространства.
Область фазового пространства, заполненного хаотическими траекториями, называется странными аттракторами.
Важнейшим свойством странных аттракторов является фрактальность. Фракталы – это объекты, проявляющие по мере увеличения все более число деталей. Хаос порождает фракталы, а фазовая траектория фракталов обладает самоподобием, т.е. при выделении двух близких точек на фазовой траектории фрактала и последующем увеличении масштаба траектория между этими точками окажется столь хаотичной, как и вся в целом. Введение фрактальных множеств позволяет объяснить и предсказать многие явления в самых различных областях.
Математические образы теории катастроф реализуются в волновых полях. Геометрическое место точек, в которых происходит фокусировка волнового поля, называется в оптике каустиками. При пересечении каустик происходит скачкообразное изменение состояния системы. Момент перехода определяется свойствами системы и уровнем флуктуации в ней. При переходе выделяют два принципа: принцип максимального промедления, определяемый существованием устойчивого уровня, и принципом Максвелла, определяющий состояние системы глобальным минимумом.
Последовательность бифуркаций, возникающая при углублении неравновесности в системе, меняется, и процесс пойдет по разным сценариям (например, переход от ламинарного течения к турбулентному).
После прохождения параметра через бифуркационное значение, соответствующее рождению цикла, или мягкому возникновению автоколебаний, система остается в окрестности неустойчивого состояния некоторое время, за которое параметр меняется на конечную величину. После этого система скачком переходит в момент бифуркации в автоколебательный режим (уже ставший жестким).
На рис.4 изображен фазовый портрет системы, описывающей взаимоотношение хищника и жертвы (скажем, щук и карасей). Фазовое пространство – положительный квадрант плоскости. По оси абсцисс отложено число карасей, по оси ординат – щук. Точка Р – положение равновесия. Точка А соответствует равновесному количеству карасей при 16 количестве щук, меньшем равновесного. Видно, что с течением времени в системе устанавливаются колебания; равновесное состояние рис. Неустойчиво. Установившиеся колебания изображаются замкнутой кривой на фазовой плоскости. Эта кривая называется предельным циклом.
В окрестности точки, не являющейся положением равновесия, разбиение фазового пространства на фазовые кривые устроено так же, как разбиение на параллельные прямые: семейство фазовых кривых можно превратить в семейство параллельных прямых заменой координат. В окрестности положения равновесия картина сложнее.
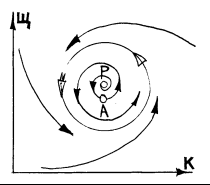
Рис.4. Фазовый портрет эволюции системы «хищник–жертва»
Системы, описывающие реальные эволюционные процессы, как правило, общего положения. Действительно, такая система всегда зависит от параметров, которые никогда не бывают известны точно.
Управление без обратной связи всегда приводит к катастрофам: важно, чтобы лица и организации, принимающие ответственные решения, лично, материально зависели от последствий этих решений.
Трудность проблемы перестройки связана с ее нелинейностью. Привычные методы управления, при которых результаты пропорциональны усилиям, тут не действуют, и нужно вырабатывать специфически нелинейную интуицию, основанную на порой парадоксальных выводах нелинейной теории.
Вот некоторые качественные простейшие выводы из математической теория перестроек применительно к нелинейной системе, находящейся в установившемся устойчивом состоянии, признанном, плохим, поскольку в пределах видимости имеется лучшее, предпочтительное устойчивое состояние системы.
1. Постепенное движение в сторону лучшего состояния сразу же приводит к ухудшению. Скорость ухудшения при равномерном движении к лучшему состоянию увеличивается.
2. По мере движения от худшего состояния к лучшему сопротивление системы изменению ее состояния растет.
3. Максимум сопротивления достигается раньше, чем самое плохое состояние, через которое нужно пройти для достижения лучшего состояния. После прохождения максимума сопротивления состояния продолжает ухудшаться.
4. По мере приближения к самому плохому состоянию на пути перестройки сопротивление, начиная с некоторого момента, начинает уменьшаться, и как только самое плохое состояние пройдено, не только полностью исчезает сопротивление, а система начинает притягиваться к лучшему состоянию.
5. Величина ухудшения, необходимого для перехода в лучшее состояние, сравнима с финальным улучшением и увеличивается по мере совершенствования системы. Слабо развитая система может перейти в лучшее состояние почти без предварительного ухудшения, в то время как развитая система, в силу своей устойчивости, на такое постепенное, непрерывное улучшение неспособна,
6. Если систему удается сразу, скачком, а не непрерывно, перевести из плохого устойчивого состояния достаточно близко к хорошему, то дальше она сама собой будет эволюционировать в сторону хорошего состояния.
Без математической теории перестроек сознательное управление сложными и плохо известными нелинейными системами практически невозможно. Не требуется, однако, специальной математической теории, чтобы понять, что пренебрежение законами природы и общества (будь то закон тяготения, закон стоимости или необходимость обратной связи), падение компетентности специалистов и отсутствие личной ответственности за принимаемые решения приводит рано или поздно к катастрофе.
Поможем написать любую работу на аналогичную тему

