Деформация (изменение расстояния) между отдельными точками среды - характерная черта движения СС.
Удлинение или укорочение произвольно направленного единичного отрезка ![]() , проходящего через точку среды М(х1,х2,х3), вычисляется по формуле
, проходящего через точку среды М(х1,х2,х3), вычисляется по формуле
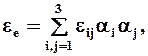 (1.19)
(1.19)
где ai = Cos (![]() ,
, ![]() ) - направляющие косинусы отрезка; eii - удлинения (укорочения) единичных отрезков, направленных параллельно координатным осям Охi ; eij = eji (i ¹ j) - изменения первоначально прямых углов, образованных отрезками, направленными параллельно координатным осям Охi , Оxj.
) - направляющие косинусы отрезка; eii - удлинения (укорочения) единичных отрезков, направленных параллельно координатным осям Охi ; eij = eji (i ¹ j) - изменения первоначально прямых углов, образованных отрезками, направленными параллельно координатным осям Охi , Оxj.
Таким образом, деформация элементарного объёма среды в окрестности точки М полностью определяется шестью величинами eij , которые называются КОМПОНЕНТАМИ СИММЕТРИЧНОГО ТЕНЗОРА ДЕФОРМАЦИЙ.
Для малых деформаций (<< 1) верны следующие соотношения Коши (в декартовой системе координат):
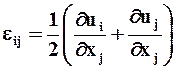 (i, j = 1,2,3), (1.20)
(i, j = 1,2,3), (1.20)
где u i- компоненты вектора перемещения в точке М.
Тройка перпендикулярных направлений, где в окрестности точки деформация элемента определяется без изменения прямых углов (eij = 0, i ¹ j), только удлинением или укорочением eij = ei , называется ГЛАВНЫМИ ОСЯМИ ДЕФОРМАЦИЙ, а величины ei (i - 1,2,3) - ГЛАВНЫМИ УДЛИНЕНИЯМИ, которые могут быть найдены из следующего соотношения
![]() ,
,
где 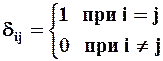 - символ Кронекера
- символ Кронекера
Коэффициенты этого уравнения не зависят от выбора системы координат, они инвариантны.
Первый коэффициент этого уравнения имеет очень простой геометрический смысл: это относительное изменение объёма в окрестности точки.
![]() . (1.21)
. (1.21)
Коэффициенты a и b геометрического смысла не имеют и поэтому не являются характеристикой деформаций.
Характеристикой искажения формы элемента сплошной среды служит инвариантная величина
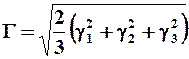 ,
,
Поможем написать любую работу на аналогичную тему

