Различают 2 этапа изучения реальных жидкостей.
1 этап - отбор тех факторов, которые являются определяющими для изучаемого процесса.
2 этап изучения - это установление зависимости интересующей величины от системы выбранных определяющих факторов. Этот этап может выполняться двумя путями: аналитическим, основанным на законах механики и физики, и экспериментальным.
Задачи позволяет решать теория гидродинамического подобия (подобия потоков несжимаемой жидкости). Гидродинамическое подобие складывается из трех составляющих; геометрического подобия, кинематического и динамического.
Геометрическое подобие – понимают подобие тех поверхностей, которые ограничивают потоки, т.е.участки русел, а также участки, которые расположены непосредственно перед ними и за ними и которые влияют на характер течения в рассматриваемых участках.
Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим через 
.Эта величина одинакова для подобных русел a и b: 
Кинематическое подобие – означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих
скоростей:
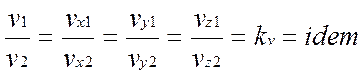
Где k - масштаб скоростей, одинаковый при кинематическом подобии.
Так как 
(где Т — время, 
- масштаб времени).
Динамическое подобие – это пропорциональность сил действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характёризующих направление этих сил.
В потоках жидкостей обычно действуют разные силы: силы давления, вязкости (трения), тяжести и др. Соблюдение их пропорциональности означает полное гидродинамическое подобие. Примем силы инерции за основу и будем другие силы, действующие на жидкость, сравнивать с инерционными общий вид закона гидродинамического подобия, число Ньютона (Ne):
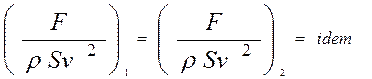
Здесь под Р подразумевается основная сила: сила давления, вязкости, тяжести или др.
Критерий 1. Число Эйлера. На жидкость действуют только силы давления и инерции. Тогда 
и общий закон имеет вид: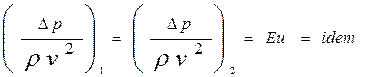 
Следовательно, условием гидродинамического подобия геометрически подобных потоков в данном случае является равенство для них чисел Эйлера.
Критерий 2. число Рейнольдса. На жидкость действуют силы вязкости, давления и инерции. Тогда 
и условие после деления последнего выражения на рv2L2 примет вид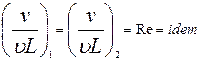 
Следовательно, условием гидродинамического подобия геометрически подобных потоков в рассматриваемом случае является равенство чисел Рейнольдса, подсчитанных для сходственных сечений потоков.
Критерий 3. число Фруда На жидкость действуют силы тяжести, давления и инерции. Тогда 
и общий закон ГП имеет вид: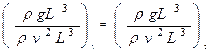 
ли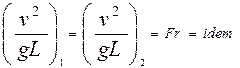 
Следовательно, условием гидродинамического подобия геометрически подобных потоков в рассматриваемом случае является равенство чисел Фруда, подсчитанных для сходственных сечений потоков.
Критерий 4:Число Вебера. При рассмотрении течений, связанных с поверхностным натяжением {распыливании топлива в двигателях) равный отношению сил поверхностного натяжения к силам инерции. Для этого случая общий закон ГП принимает вид:
Критерий 5. Число Струхаля. При рассмотрении неустановившихся (нестационарных) периодических течений с периодом Т (например, течений в трубопроводе, присоединенном к поршневому насосу), учитывает силы инерции от нестационарности, называемые локальными. Последние пропорциональны массе (рL3) и ускорению которое, в свою очередь, пропорционально 
.Следовательно, общий закон ГП принимает вид
или 
Критерий 6. Число Маха. При рассмотрении движений жидкости с учетом ее сжимаемости (например, движений эмульсий). Учитывает силы упругости. Последние пропорциональны площади (L2) и объемному модулю упругости К =
. Поэтому силы упругости пропорциональны
Поможем написать любую работу на аналогичную тему