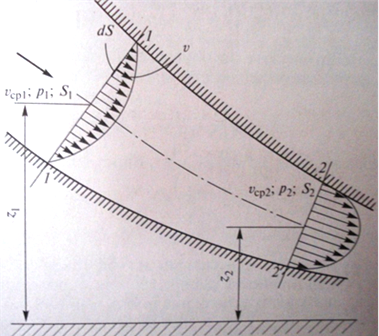
Пусть поток реальной жидкости, обладающий вязкостью, движется в русле, ограниченном неподвижными стенками. Будем основываться на том, что уравнение Бернулли является законом сохранения энергии для движущейся жидкости. На первом этапе учтём неравномерность распределения скоростей по сечению потока, на втором – и потери энергии. Будем считать, что 
(справедливо только для плоских сечений). Полный напор сечения 1-1 струйки жидкости 
. Мощность струйки dN в сечении площадью dS: 
(QG = Qm 
=Q
). Мощность всего потока: 
. После преобразований: 
, где 
– безразмерный коэффициент: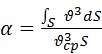 
. Этот коэффициент (Кориолиса) учитывает неравномерность распределения скорости потока жидкости в сечении реального потока (физический смысл: а – отношение действительной кинетической энергии реального потока в данном сечении к кинетической энергии того же потока в том же сечении, но посчитанной по средней скорости жидкости в данном сечении). 
. В реальных потоках из-за потерь при движении жидкости среднее значение полного напора в конечном сечении, поэтому 
или
(1) – уравнение Бернулли для потока реальной жидкости.
– поток идеальной жидкости, 
.
, где 
– безразмерный коэф-т, определяющий потери в данном местном сопротивлении,
– средняя скорость в трубопроводе, в котором установлено местное сопротивление,
– безразмерный коэффициент потерь на трение по длине (коэф-т Дарси).
Поможем написать любую работу на аналогичную тему