Истечение жидкости через отверстие при переменном напоре. Время опорожнения сосуда.

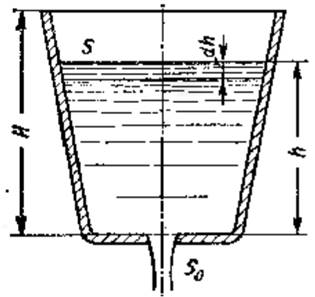
Рассмотрим опорожнение открытого в атмосферу сосуда произвольной формы через донное отверстие или насадок с коэффициентом . В этом случае истечение будет происходить при переменном, постепенно уменьшающемся напоре, т. е., строго говоря, течение является неустановившимся. Однако если напор, а, следовательно, и скорость истечения изменяется медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли (квазистационарное течение). Обозначив переменную высоту уровня жидкости в сосуде, отсчитываемую от дна, через , площадь сечения резервуара на этом уровне , а площадь отверстия  и взяв бесконечно малый отрезок времени  можно записать следующее уравнение объёмов.  или  где  - изменение уровня жидкости в сосуде за время  Знак минус обусловлен тем, что положительному приращению  соответствует отрицательное приращение . Отсюда время полного опорожнения сосуда высотой  найдём следующим путём (считая )  Интеграл можно посчитать если известен закон изменения площади  по высоте . Для призматического резервуара, у которого , следовательно,  Числитель этой формулы равен удвоенному объёму сосуда, а знаменатель представляет собой расход в начальный момент опорожнения, т. е. при напоре . Следовательно, время полного опорожнения сосуда в 2 раза больше времени истечения того же объёма жидкости при постоянном напоре, равном первоначальному.