До сих пор рассматривались давления, действующие в жидкости. Однако более важное практическое значение имеют силы, возникающие от действия жидкости на различные стенки.
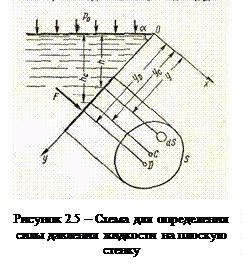
При определении силы, действующей со стороны жидкости на плоскую стенку, рассмотрим общий случай, когда стенка наклонена к горизонту под углом α, а на свободную поверхность жидкости действует давление р0 (рисунок 2.5).
Вычислим силу давления F, действующую на некоторый участок рассматриваемой стенки площадью S. Ось Ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось Оу — перпендикулярно к этой линии в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS:
dF = p dS = (pо + ρ gh) dS = pо dS + ρ g h d S,
где ро — давление на свободной поверхности;
h — глубина расположения площадки dS.
Для определения полной силы F проинтегрируем полученное выражение по всей площади S:
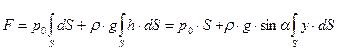
где у — координата площадки dS.
Последний интеграл представляет собой статический момент площади S относительно оси Ох и равсн произведению этой площади на координату ее центра тяжести (точка С), то есть
,
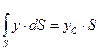Следовательно
,
здесь hс — глубина расположения центра тяжести площади S.
Поможем написать любую работу на аналогичную тему