Сила давления жидкости на плоскую стенку - Основы гидравлики

Рассмотрим вопрос о силе давления жидкости на плоскую стенку площадью  S, расположенную под произвольным углом a к горизонту и ограниченную произвольным контуром (Рис.13). Как известно, сила характеризуется тремя параметрами:

– направлением:

– величиной;

– точкой приложения.

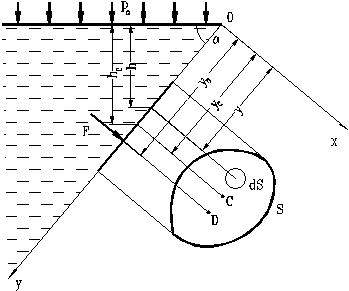
Рис. 13. Схема для определения силы давления жидкости

на плоскую стенку

Давление в каждой точке стенки направлено по нормали к ней, следовательно, и равнодействующая сила давления будет перпендикулярна плоской стенке.

Ось 0x направим по линии пересечения стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно к этой линии в плоскости стенки.

Вычислим элементарную силу давления, приложенную к бесконечно малой площадке dS:

,

где p0 – давление на свободную поверхность;

      h – глубина расположения площадки dS.

Для получения полной силы давления F проинтегрируем полученное выражение по всей площади S:

.

Полученный интеграл представляет собой статический момент площади S относительно оси 0x и равен произведению этой площади на координату ее центра масс (точка С), то есть

.

Следовательно,

,

где hC, pC – глубина расположения центра масс площадки и давление в этой точке.

Таким образом, полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление pC в центре масс этой площади.

Силу давления F можно представить как сумму двух сил: F0  от внешнего давления p0 и силы Fж от веса жидкости, то есть

F = F0 + Fж = (p0 + pC)S.

Если давление p0 равно атмосферному и действует также с обратной стороны стенки, то сила избыточного давления жидкости на плоскую стенку

Fизб = Fж = grhCS = pC изб S.

Наиболее сложным является вопрос о точке приложения силы давления на плоскую стенку. Сила F0 будет приложена в центре масс плоской стенки C, так как давление p0 действует на все точки стенки одинаково. Точка приложения силы Fж отыскивается путем составления уравнения моментов равнодействующей и составляющих сил относительно горизонтальной оси, например, совпадающей с линией пересечения стенки со свободной поверхностью:

.

Выразим координату точки приложения силы yD и подставим значения сил Fж  и dFж:

,

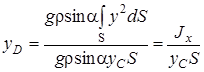где  – момент инерции площади S относительно оси 0x.

Учитывая, что

где Jx0 – момент инерции площади S относительно горизонтальной оси, лежащей в плоскости стенки и проходящей через ее центр масс.

Отсюда, точка приложения силы Fж имеет координату

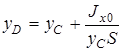
Если давление p0 равно атмосферному, центр давления будет находиться в точке D. Как видно из формулы, yD лежит ниже центра масс площади S. Если внешнее давление p0 > pатм, то равнодействующая будет приложена выше т. D и наоборот. Точное ее место приложения вычисляют из уравнения моментов.