Если в гидродинамическом поле отсутствуют вихри, то; для такого поля можно записать уравнение, связывающее параметры движущейся жидкости (плотность жидкости) с
параметрами, характеризующими условия движения жидкости. Вывод такого уравнения основан на представлении жидкости как сплошной непрерывной среды, в силу чего такое уравнение получило название уравнения неразрывности.
Для этой цели выделим в пространстве малый элемент жидкой среды в виде параллелепипеда, стороны которого будут равны соответственно.
. Грани параллелепипеда пусть будут параллельны координатным плоскостям. В центре элемента в данный момент времени будет находиться частица жидкости, плотность которой равна р, а вектор скорости движения и направлен таким образом, что жидкость втекает внутрь элемента через левую, нижнюю и переднюю грани элемента и вытекает через противоположные грани.
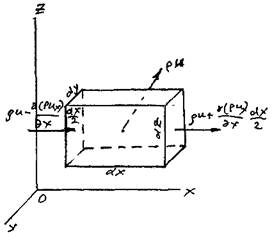
Будем считать также, что размер элемента достаточно мал, и можно допустить, что в пределах этого элемента изменение плотности жидкости и скорости её движения будет прямо пропорционально расстоянию от центра элемента. Одновременно размеры граней будут достаточно велики по сравнению с точкой, что позволит утверждать, что плотность жидкости и скорость во всех точках граней будут одинаковыми, как и плотность жидкости в пределах соответствующих граней. Тогда произведение плотности жидкости на вектор скорости (импульс) в специальной литературе часто называют вектором массовой скорости ри.
В таком случае проекция вектора массовой скорости в центре левой грани элемента на ось ОХ будет равна:
а проекция вектора массовой скорости в центре правой грани элемента на ось ОХ:
&
Масса жидкости, поступившая через левую грань элемента за малый интервал времени dt
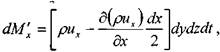
масса жидкости, вытекшая через правую грань элемента за малый интервал времени dt:
Изменение массы жидкости внутри элемента при движении жидкости вдоль оси ОХ:
Аналогично, изменение массы жидкости внутри элемента при движении жидкости вдоль оси OY: 1,
и вдоль оси OZ:
Окончательно, изменение массы жидкости внутри элемента при движении жидкости в произвольном направлении:
? или
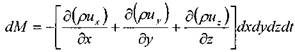
Величина плотности жидкости в начальный момент (до начала движения жидкости t = Q) - р, а по истечении бесконечно малого интервала времени (т.е.
Масса жидкости в объёме выделенного элемента в начальный момент времени:
для времени
:
Изменение массы жидкости за бесконечно малый интервал времени dt:
•> или:
i
откуда для наиболее общего случая нестационарного поля
дифференциальное уравнение неразрывности запишется в следующем виде:
и для частного случая - стационарного поля
:
«
В векторной форме уравнения неразрывности жидкости запишутся в следующем виде:
?
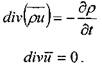Поможем написать любую работу на аналогичную тему