Уравнение неразрывности или сплошной жидкости основано на законе сохранения массы и исходит из положения механики сплошных сред о том, что в нутрии движущейся жидкости не может произойти разрыв, т. е. установится пустота.
Уравнение неразрывности может быть представлено в дифференциальной форме для частицы жидкости и элементарной струйки, а также в конечных величинах для потока жидкости.
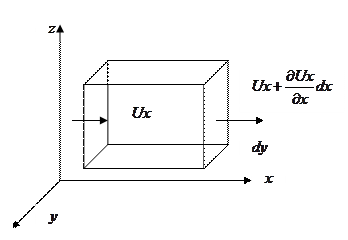
Выделим в потоке элементарный объем. Рассмотрим изменение протекающей массы жидкости по оси Ox. Скорость жидкости вытекающей через левую грань Ux, тогда скорость вытекающей через правую 
Принимая ρ=const, можно записать, что через0 левую грань за время dt пройдет масса
;
( где Uxdt=dx; 
)
А через правую 
Разность этих масс составит 
Рассматривая по аналогии изменение массы жидкости по осям Oy и Oz, запишем 
и 
Закон сохранения массы требует, чтобы общее изменение массы, прошедшей через выбранный объем, равнялось нулю
=0
Или 
(4.3)
Уравнение (4.3) называется уравнением неразрывности или сплошности в дифференциальной форме для произвольного движения не6сжимаемой жидкости.
При установившемся движении уравнение неразрывности можно вывести исходя из свойств элементарной струйки, в соответствии с которым жидкость из струйки не вытекает в стороны и не притекает в нее извне, но в то же время местные скорости разные по длине струйки. Отсюда следует, что количество жидкости, притекающей к струйке в начальном сечении и вытекающей из нее в конечном сечении, равны между собой и общий объем жидкости в струйке не изменяется т. е. элементарные расходы в единицу времени:
втекает 
,
вытекает 
и тогда 
(4.4)
Выражение (4.4) и является уравнением неразрывности для элементарной струйки.
Для потока жидкости уравнение неразрывности будет иметь вид:
или 
Т. е. отношение средних скоростей в сечениях потока обратно пропорционально отношению их площадей. Из этого следует, что при установившемся сечении с уменьшением площади сечения средняя скорость увеличивается и наоборот.
Поможем написать любую работу на аналогичную тему