Вывод основных гидродинамических уравнений начнём с вывода уравнения неразрывности, выражающего закон сохранения в гидродинамике.
Математическое описание состояния движущейся жидкости осуществляется с помощью функций, определяющих распределение скоростей ![]() и каких-либо двух термодинамических величин, например,
и каких-либо двух термодинамических величин, например, ![]() - давления и
- давления и ![]() - плотности.
- плотности.
Скорость, давление и плотность жидкости будем относить к данным точкам пространства, а не к определённым частицам жидкости, передвигающимся во времени и в пространстве. То есть будем пользоваться переменными Эйлера.
|
|
Рассмотрим некоторый объём Vo пространства. Количество (масса) жидкости в этом объёме есть
Через элемент поверхности
|
Вектор ![]() по абсолютной величине равен площади элемента поверхности и направлен по внешней нормали к ней. Тогда
по абсолютной величине равен площади элемента поверхности и направлен по внешней нормали к ней. Тогда ![]() положительно, если жидкость вытекает из объёма, и отрицательно, если жидкость втекает в него.
положительно, если жидкость вытекает из объёма, и отрицательно, если жидкость втекает в него.
Полное количество жидкости, вытекающей в единицу времени из объёма Vo
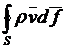 .
.
где S - поверхность, ограничивающая выделенный объём Vo.
С другой стороны, уменьшение количества жидкости в объёме Vo можно записать в виде
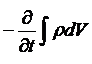 .
.
Приравнивая оба выражения, получаем:
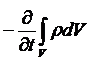
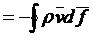 .
.
Интеграл по поверхности преобразуем в интеграл по объёму
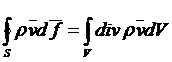 .
.
Таким образом,
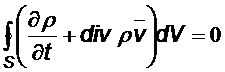 .
.
Поскольку это равенство должно иметь место для любого выделенного объёма, то должно быть равным нулю подынтегральное выражение, т.е.
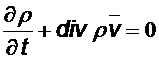 .
.
Получили уравнение неразрывности.
Расписав выражение ![]() можно записать
можно записать
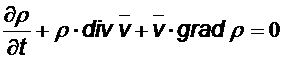
![]()
В декартовых координатах
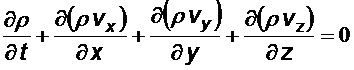 .
.
Вектор ![]() называют плотностью потока жидкости.
называют плотностью потока жидкости.
Его направление совпадает с направлением движения жидкости, а абсолютная величина определяет количество жидкости, протекающей в единице времени через единицу площади, расположенной перпендикулярно к скорости.
Поможем написать любую работу на аналогичную тему


 Рис. 11
Рис. 11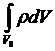 .
.