Сохранение циркуляции скорости

          Интеграл

,

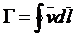взятый вдоль замкнутого контура, называют циркуляцией скорости вдоль этого контура.

          Рассмотрим некоторый замкнутый контур, проведенный в жидкости в некоторый момент времени. Будем рассматривать его как "жидкий", составленный из находящихся на нём частиц жидкости. С течением времени контур перемещается.

          Вычислим производную по времени от циркуляции скорости с учётом подвижности контура. Временно дифференцирование по координатам обозначим знаком , знак - дифференцирование по времени. Будем учитывать, что меняются скорость и сам контур.

.

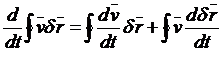По определению скорость  это производная радиус-вектора

.

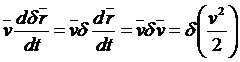          Интеграл по замкнутому контуру от полного дифференциала равен нулю и остаётся

.

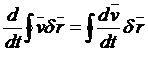          Из уравнений Эйлера имеем

.

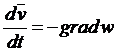          Применим формулу Стокса, получаем тогда (поскольку )

.

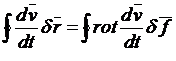          Таким образом, переходя к прежним обозначениям, находим окончательно:

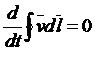   ,  или  .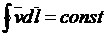

          Мы приходим к результату, что в идеальной жидкости циркуляция скорости вдоль замкнутого контура остаётся неизменной со временем.

          Это утверждение называется теоремой Томсона или законом сохранения циркуляции скорости. Соотношение получено путём использования уравнений Эйлера и предположения об изэнтропичности движения жидкости.

          Применим теорему Томсона к бесконечно малому замкнутому контуру и, преобразовав интеграл по теореме Стокса, получим:

,

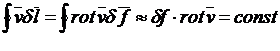где - элемент поверхности, опирающейся на контур . Вектор  часто называется завихренностью течения жидкости в данной её точке. Постоянство произведения  можно использовать, сказав, что завихренность переносится вместе с движущейся жидкостью.