Движение жидкости, при котором во всём пространстве 
называется потенциальным (или безвихревым) в противоположность вихревому движению, при котором ротор скорости отличен от нуля.
|
Рис. 13 |
Таким образом, мы пришли бы к выводу, что стационарное обтекание взятого тела натекающим из бесконечности однородным потоком должно быть потенциальным ( рис. 13 ). Поскольку на бесконечности натекающий поток однороден, его скорость |
, так что 
на всех линиях тока.Однако, ввиду наличия стенки нельзя провести в жидкости замкнутый контур, который охватывал бы такую линию тока.
В результате возникает картина течения, характеризующаяся наличием отходящей от тела "поверхности тангенциального разрыва", на которой скорость жидкости терпит разрыв непрерывности.
Как и всякое векторное поле с равным нулю ротором, скорость потенциально движущейся жидкости может быть выражена в виде градиента от некоторого скаляра, называемого потенциалом скорости 
.
Напишем уравнения Эйлера в виде
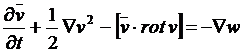
и подставив в него
, получаем
.
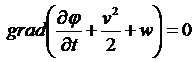Откуда находим следующее равенство
,
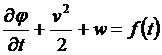где
произвольная функция времени. Это равенство представляет собой первый интеграл уравнений потенциального движения.
При стационарном движении имеем 
, 
и интеграл переходит в уравнение Бернулли
.
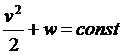Отметим существенные отличия между уравнениями Бернулли в случае потенциального и непотенциального движения константа в правой части этого уравнения есть величина, постоянная вдоль каждой линии тока, но вообще говоря, различная для разных линий тока.
При потенциальном же движении константа в уравнении Бернулли есть величина, постоянная во всём объёме жидкости.
Поможем написать любую работу на аналогичную тему