Для плоских течений жидкостей их плотность можно считать постоянной вдоль всего объёма жидкости в течение всего времени движения. Такое движение называется движением несжимаемой жидкости.
Общие уравнения гидродинамики для несжимаемой жидкости упрощаются. Уравнение неразрывности при ![]() принимает простой вид
принимает простой вид
![]() .
.
уравнения Эйлера не меняют своего вида, запишем их в виде
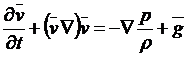 .
.
Для несжимаемой жидкости тепловая функция записывается следующим образом
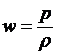 .
.
Тогда уравнение Бернулли для несжимаемой жидкости имеет вид
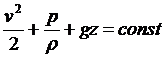 .
.
Особенно упрощается уравнение для потенциального течения несжимаемой жидкости.
При подстановке ![]() в уравнение неразрывности
в уравнение неразрывности ![]() , получим
, получим
![]() ,
,
то есть уравнение Лапласа для потенциала.
Граничные условия. К этому уравнению должны быть добавлены граничные условия на поверхности соприкосновения жидкости с твёрдыми телами:
- на неподвижных твёрдых поверхностях нормальная к поверхности компонента vn скорости жидкости должна быть равна нулю, для движущихся тел vn должна быть равна проекции скорости движения тела на направление той же нормали.
С другой стороны, скорость vn равна производной от потенциала![]() по направлению нормали
по направлению нормали
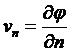 .
.
Таким образом, граничные условия гласят в общем случае, что![]() является на границах заданной функцией координат и времени.
является на границах заданной функцией координат и времени.
При потенциальном движении скорость связана с давлением для несжимаемой жидкости соотношением
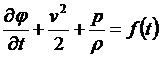 .
.
Если движение жидкости является потенциальным и вызвано движением некоторого тела то уравнение Лапласа не содержит явно времени, время входит в решение через граничные условия.
|
Рис. 14 |
Из уравнения Бернулли |
Если U - скорость набегающего на тело потока жидкости (скорость на бесконечности), а p0 – давление на бесконечности, то давление в критической точке равно
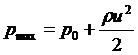 .
.
Если распределение скоростей в движущейся жидкости зависит только от двух координат, то о таком течении говорят как о двумерном или плоском. Для решения задач о двумерном течении несжимаемой жидкости иногда удобнее использовать функцию тока. Из уравнения неразрывности
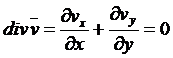
видно, что компоненты скорости могут быть записаны в виде производных
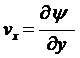 ,
, 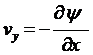
от некоторой функции ![]() , называемой функцией тока. Уравнение неразрывности при этом удовлетворяется автоматически.
, называемой функцией тока. Уравнение неразрывности при этом удовлетворяется автоматически.
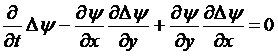 .
.
Зная функцию тока, можно непосредственно определить форму линий тока для стационарного движения жидкости. Дифференциальное уравнение линий тока
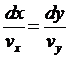
или
![]() ,
,
оно выражает условие параллельности касательной к линии тока и направления вектора скорости.
Подставляя сюда выражение для скоростей через функцию тока
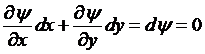 ,
,
откуда![]() . Таким образом, линии тока представляют собой семейство кривых, получающихся приравниванием функции тока
. Таким образом, линии тока представляют собой семейство кривых, получающихся приравниванием функции тока ![]() постоянной.
постоянной.
Если между точками 1 и 2 в плоскости x,y провести кривую, то поток жидкости Q через эту кривую определится разностью значений функции тока в этих точках независимо от формы кривой.
Действительно, если vn - проекция скорости на нормаль к кривой в данной точке, то
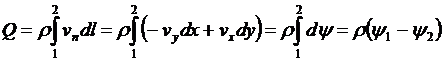
или
![]() .
.
Мощные методы решения задач о простом потенциальном обтекании несжимаемой жидкостью различных профилей связаны с применением к ним теории функций комплексной переменной.
Поможем написать любую работу на аналогичную тему


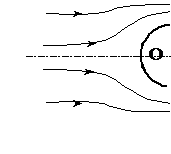
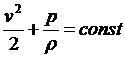 видно, что при стационарном движении несжимаемой жидкости вне поля тяжести наибольшее значение давления достигается в точках, где скорость обращается в нуль. Такая точка обычно имеется на поверхности обтекаемого жидкостью тела (точка О) и называется критической точкой.
видно, что при стационарном движении несжимаемой жидкости вне поля тяжести наибольшее значение давления достигается в точках, где скорость обращается в нуль. Такая точка обычно имеется на поверхности обтекаемого жидкостью тела (точка О) и называется критической точкой.