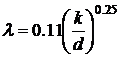Теоретические и экспериментальные исследования показывают, что потери напора на трение по длине вычисляются по формуле Дарси-Вейсбаха
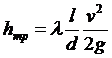 ,
,
где l- расстояние между рассматриваемыми сечениями, т.е. длина трубы, v - скорость течения, d- внутренний диаметр трубы, ![]() - коэффициент гидравлических потерь на трение по длине,
- коэффициент гидравлических потерь на трение по длине, 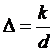 - относительная шероховатость.
- относительная шероховатость.
Для ламинарного режима движения жидкости
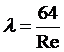 .
.
Основные два вопроса, которые интересуют инженера при рассмотрении турбулентного движения жидкости в трубах:
1) определение потерь напора,
2) распределение скоростей по поперечному сечению трубы.
Потери напора и распределение скоростей могут сильно меняться в зависимости от диаметра трубы, скорости движения, вязкости жидкости и шероховатости стенок труб.
Для учета шероховатости используют понятие относительной шероховатости:
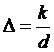 .
.
|
|
Шези предложил:
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
где с - коэффициент Шези,
формула Шези. |
Cистематические опыты для выяснения характера зависимости коэффициента гидравлического трения от числа Re
Рейнольдса и шероховатости 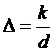 были проведены H.Hикурадзе в 1933 в гладких трубах с искусственной равномерно-зернистой шероховатостью из кварцевого песка oт
были проведены H.Hикурадзе в 1933 в гладких трубах с искусственной равномерно-зернистой шероховатостью из кварцевого песка oт ![]() = 0.00197 до 0.066. При различных расходах измерялась потеря напора и вычислялся коэффициент l по формуле Дарси-Вейсбаха.
= 0.00197 до 0.066. При различных расходах измерялась потеря напора и вычислялся коэффициент l по формуле Дарси-Вейсбаха.
Результаты опытов Hикурадзе представлены на рис. 45 в виде графика зависимости величины lg(100l) от числа lg(Re).
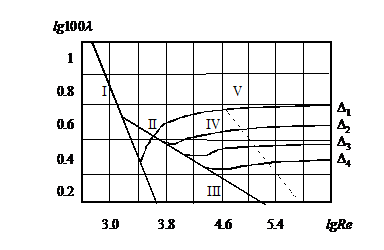
Рис. 45
|
№ |
Наименование зоны |
Re |
l |
Примечание |
|
I |
Ламинарная |
0<Re<2300 |
|
Движение зависит только от Re |
|
II |
Переходная |
2300<Re<4000 |
|
|
|
III |
Гидравлически гладкие трубы |
|
Формула Блазиуса
|
|
|
IV |
Шероховатые трубы |
|
Формула Альтшуля
|
|
|
V |
Зона автомодель-ности |
|
Формула Шифрисона
|
|
При ламинарном режиме (Re<2000, или lg(Re)<3.3) точки, независимо от шероховатости стенок, ложатся на прямую линию I. При ламинарном режиме движения шероховатость не оказывает влияния на сопротивление.
При турбулентном режиме (Re>2000, или lg(Re)>3.3) точки ложатся на линию III, полученную при испытании гладких труб без искусственной шероховатости. Малые шероховатости не оказывают влияния на сопротивление трубы при турбулентном движении.
При больших числах Рейнольдса коэффициент гидродинамического трения перестает зависеть от числа Рейнольдса (то есть от вязкости жидкости) и для данного значения ![]() сохраняет постоянную величину.
сохраняет постоянную величину.
Полученные результаты могут иметь следующее физическое истолкование. При малых числах Рейнольдса жидкость обтекает выступы шероховатости без образования и отрыва вихрей благодаря значительному влиянию вязкости жидкости, свойства поверхности стенок труб не оказывают при этом влияния на сопротивление и кривые ![]() совпадают с прямой.
совпадают с прямой.
С увеличением скорости (т.е. числа Рейнольдса) от бугорков шероховатости начинают отрываться вихри, свойства поверхности уже оказывают влияние на сопротивление и кривые ![]() отклоняются от линии гладкого трения.
отклоняются от линии гладкого трения.
В результате многочисленных исследований были предложены различные эмпирические формулы для определения коэффициента гидравлического трения.
Для гидравлически гладких труб широкое распространение получили формула Блазиуса
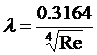 ,
,
а для вполне шероховатых труб - формулы Шифринсона
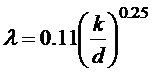 .
.
Поможем написать любую работу на аналогичную тему


 Рис. 44
Рис. 44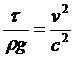 ;
; 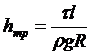 ;
; 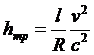
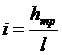 ;
; 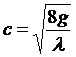 ;
; 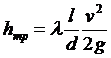 ;
; 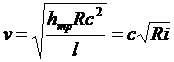 -
-