1. Однородный равномерный поток
Рассмотрим плоское прямолинейное и равномерное установившееся течение несжимаемой жидкости с одинаковой во всём потоке скоростью vx, параллельной оси ox. В этом случае
![]() .
.
Отсюда
![]() .
.
![]() Линии равных потенциалов j=const представляют собой прямые, параллельные оси ординат.
Линии равных потенциалов j=const представляют собой прямые, параллельные оси ординат.
Можно положить jo= 0 и k = 0, тогда
![]() .
.
Функцию тока найдём из условия
![]() .
.
Сетка такого плоского течения изображается семейством ортогональных прямых, параллельных осям координат, а комплексный потенциал равен
![]() .
.
Для прямолинейного течения несжимаемой невязкой жидкости со скоростью v, наклонённой к оси абсцисс под углом a, будем иметь
![]() .
.
Откуда
![]()
и
![]() ,
,
![]() .
.
Комплексный потенциал такого течения будет иметь вид
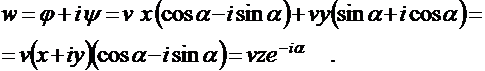
2. Источник и сток
В качестве следующего примера рассмотрим течения, которые носят название источника и стока.
Пусть невязкая несжимаемая жидкость непрерывно возникает в некоторой точке Р и вытекает в неограниченное пространство с постоянным расходом Q и с одинаковой интенсивностью во всех направлениях ( рис. 59 ). Линии тока этого воображаемого источника будут представлять собой прямые, расходящиеся из точки Р. Это характеризует пространственный источник.
Источник Сток
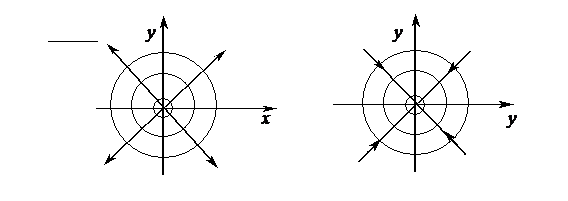
а б
Рис. 59
Если жидкость течёт из неограниченного пространства в точку, где непрерывно исчезает, течение называется пространственным стоком.
Рассмотрим плоский источник и проведём из него как из центра несколько концентрических окружностей различного радиуса. Уравнение неразрывности - уравнение постоянства расхода через любую концентрическую цилиндрическую поверхность, имеющую высоту, равную единице, в случае несжимаемой жидкости будем иметь
![]() .
.
Отсюда скорость
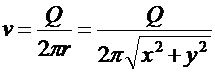
и, следовательно,
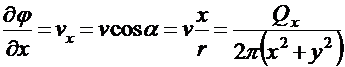 ,
,
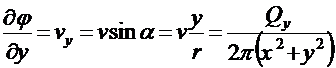 .
.
Откуда
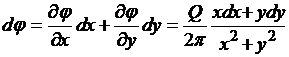 .
.
Интегрируя
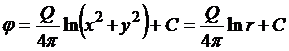 ,
,
где С - константа интегрирования, которая может быть принята равной нулю, если полагать, что на круге r = 1 функция j = 0.
Для определения функции тока воспользуемся выражением
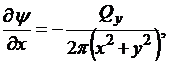
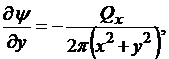
откуда полный дифференциал
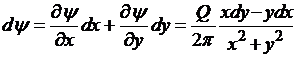 .
.
После интегрирования имеем
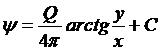 ,
,
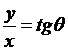 и С = 0 при y = 0.
и С = 0 при y = 0.
Следовательно
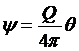 .
.
Потенциал скорости источника j(r) может быть интерпретирован в виде семейства концентрических кругов различного радиуса, а функция тока y(q) в виде пучка прямых, исходящих из источника.
3. Вихрь
Рассмотрим комплексный потенциал
![]() .
.
Пусть А - действительное число
![]() ,
,
![]() ,
,
![]() .
.
Линии тока лучи e=const . Изопотенциальные линии - окружности.
Найдём расход
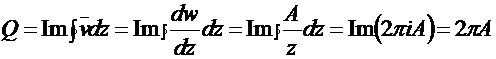 ,
,
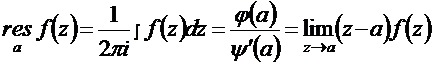 ,
,
![]() ,
, ![]()
- комплексный потенциал источника или стока мощности Q ( рис. 60 ).
Пусть А - чисто мнимое равное Вi, где В - действительное.
![]()
Источник Вихрь
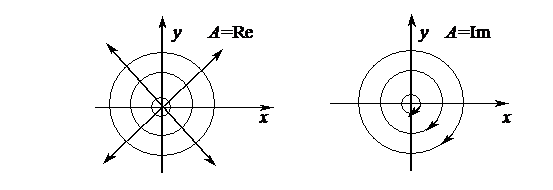
а б
Рис. 60
![]() ,
,
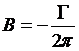 ,
,
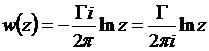 - вихрь.
- вихрь.
4. Вихреисточник
Рассмотрим случай комплексного коэффициента при логарифме
![]() .
.
|
|
Такой комплексный потенциал можно рассматривать как результат наложения двух потоков
- комплексный потенциал вихреисточника ( рис. 61 ). |
5. Диполь
Рассмотрим комплексный потенциал ![]() ,
,
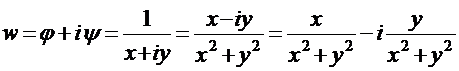 ,
,
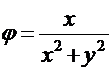 ,
, 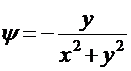 .
.
Найдём семейство линий тока
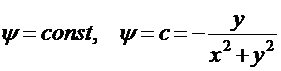 ,
,
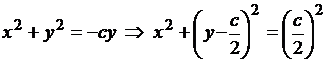 .
.
Линии тока - окружности с центрами на оси oy.
|
Рис. 62 |
Изопотенциальные линии - окружности с центрами на оси ox( рис. 62 ). Диполь
где m - момент диполя. |
Поможем написать любую работу на аналогичную тему


 Рис. 61
Рис. 61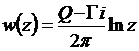

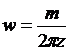 ,
,